Quantum Skyrmion Lattices
in Heisenberg Ferromagnets
Andreas Haller, Solofo Groenendijk, Alireza Habibi, Andreas Michels and Thomas L. Schmidt



Luxembourg City
Belval Campus
Outline
Introduction

Tensor Networks

Quantum Spin Model
Classical Skyrmions
- quasiparticles in non-centrosymmetric thin films
- Heisenberg & Dzyaloshinskii-Moriya interaction
- spin winding with quantized topological index
- robust & long lifetimes: stable against disorder, high temperatures
Quantum Skyrmions
- quasiparticles in non-centrosymmetric thin films
- Heisenberg & Dzyaloshinskii-Moriya interaction
- topological witness (not quantized!)
- more or less robust?
- how much ''classical'' are the quantum states?
Classical Spin Model
\[ E = \overbrace{ J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} }^{\rm Heisenberg} + \overbrace{ \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\bm S_{\bm r_i}\times\bm S_{\bm r_j} }^{\rm Dzyaloshinskii-Moriya} \\ \underbrace{ +\sum_{i}\bm B_{\bm r_i}\cdot\bm S_{\bm r_i} }_{\rm external\ Zeeman\ Field} \]Heisenberg
\[ E_J(\{\bm S_{\bm r_i},\ i=1,...,N\}) = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} \]
\(J > 0\)

numerically find \(\min_{\{\bm S_{\bm r_i},\ i=1,...,N\}}E_J\)
Heisenberg
\[ E_J(\{\bm S_{\bm r_i},\ i=1,...,N\}) = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} \]
\(J > 0\)

numerically find \(\min_{\{\bm S_{\bm r_i},\ i=1,...,N\}}E_J\)
Heisenberg
\[ E_J(\{\bm S_{\bm r_i},\ i=1,...,N\}) = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} \]
\(J < 0\)

numerically find \(\min_{\{\bm S_{\bm r_i},\ i=1,...,N\}}E_J\)
Heisenberg
\[ E_J(\{\bm S_{\bm r_i},\ i=1,...,N\}) = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} \]
\(J < 0\)
 \(J>0\)
\(J>0\)

Dzyaloshinskii-Moriya (DM)
\[ E_D(\{\bm S_{\bm r_i},\ i=1,...,N\}) = \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\bm S_{\bm r_i}\times\bm S_{\bm r_j} \]
\(\bm D_{\bm r_i,\bm r_j} = |D|\hat e_z\times(\bm r_j-\bm r_i)\)

DM vs. Heisenberg
\[ E_{J,D} = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} + \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\bm S_{\bm r_i}\times\bm S_{\bm r_j} \]
\(\bm D_{\bm r_i,\bm r_j} = |D|\hat e_z\times(\bm r_j-\bm r_i)\)

DM vs. Heisenberg
\[ E_{J,D} = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} + \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\bm S_{\bm r_i}\times\bm S_{\bm r_j} \]
\(\bm D_{\bm r_i,\bm r_j} = |D|\hat e_z\times(\bm r_j-\bm r_i)\)
DM vs. Heisenberg
\[ E_{J,D} = J \sum_{\braket{i,j}} \bm S_{\bm r_i}\cdot\bm S_{\bm r_j} + \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\bm S_{\bm r_i}\times\bm S_{\bm r_j} \]
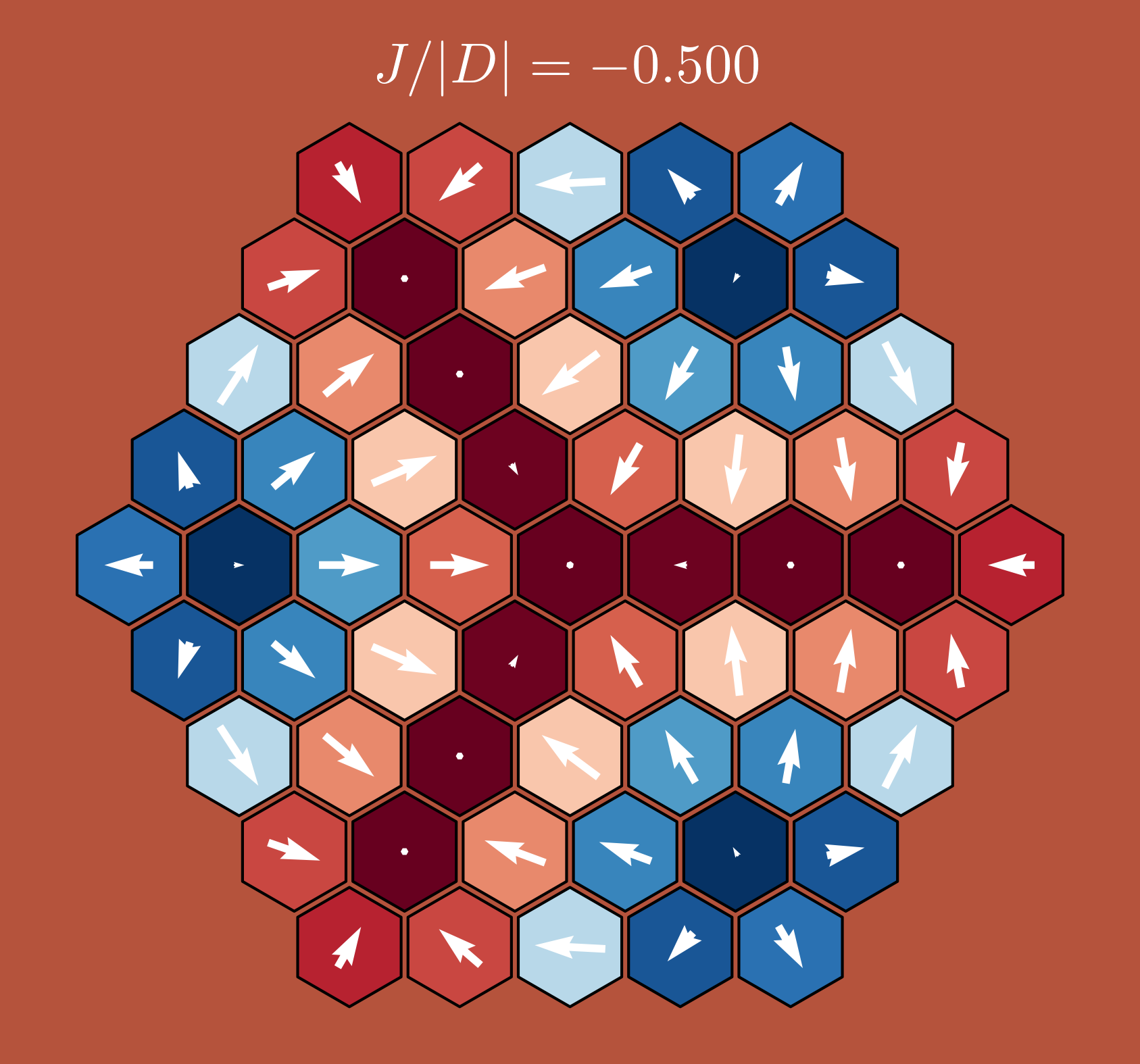

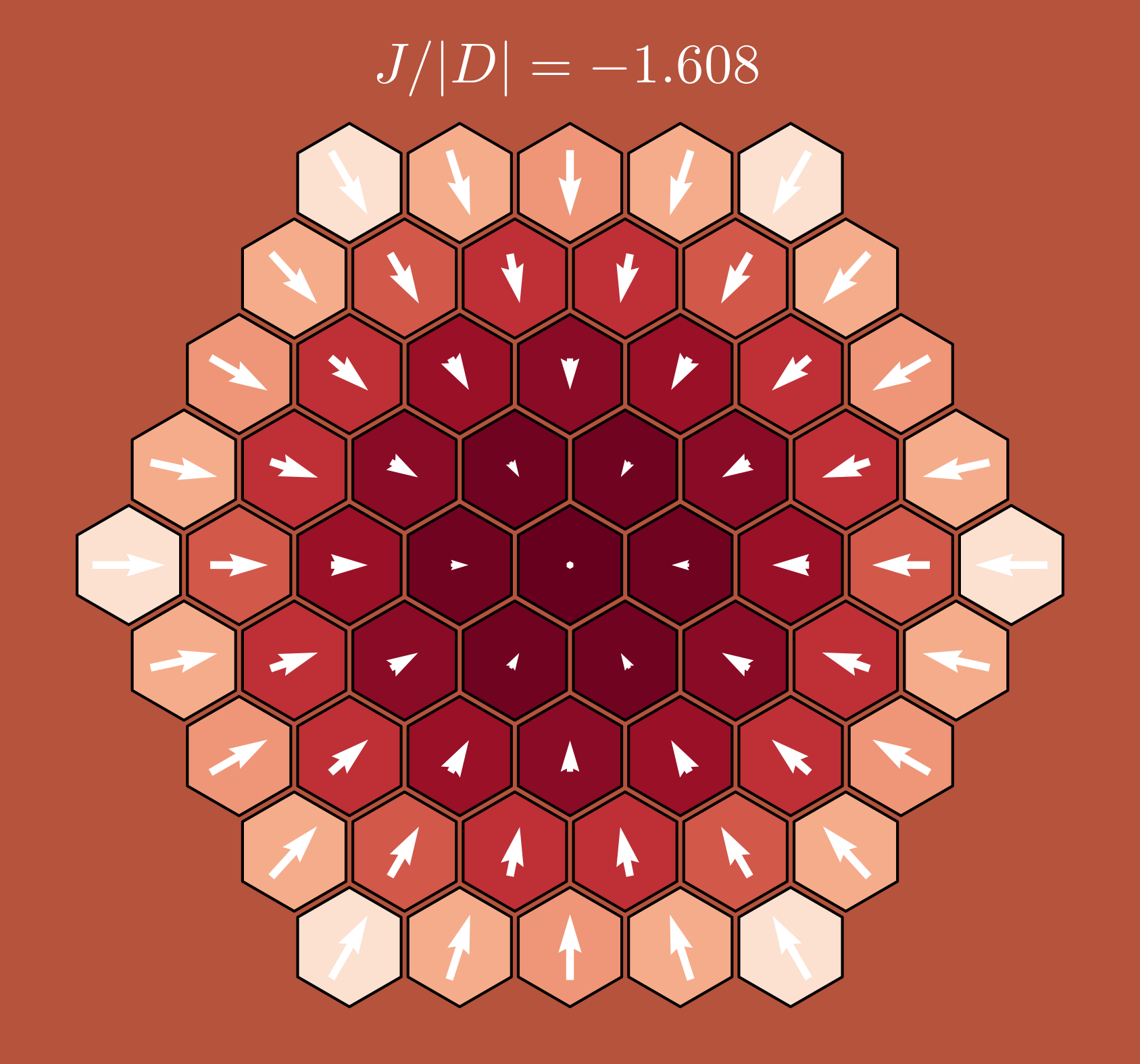
DM vs. Heisenberg vs. Zeeman
\[ E_{J,B,D} = E_{J,D} + \sum_{\bm r}\bm B_{\bm r}\cdot\bm S_{\bm r} \]
$ J = -0.5|D| $
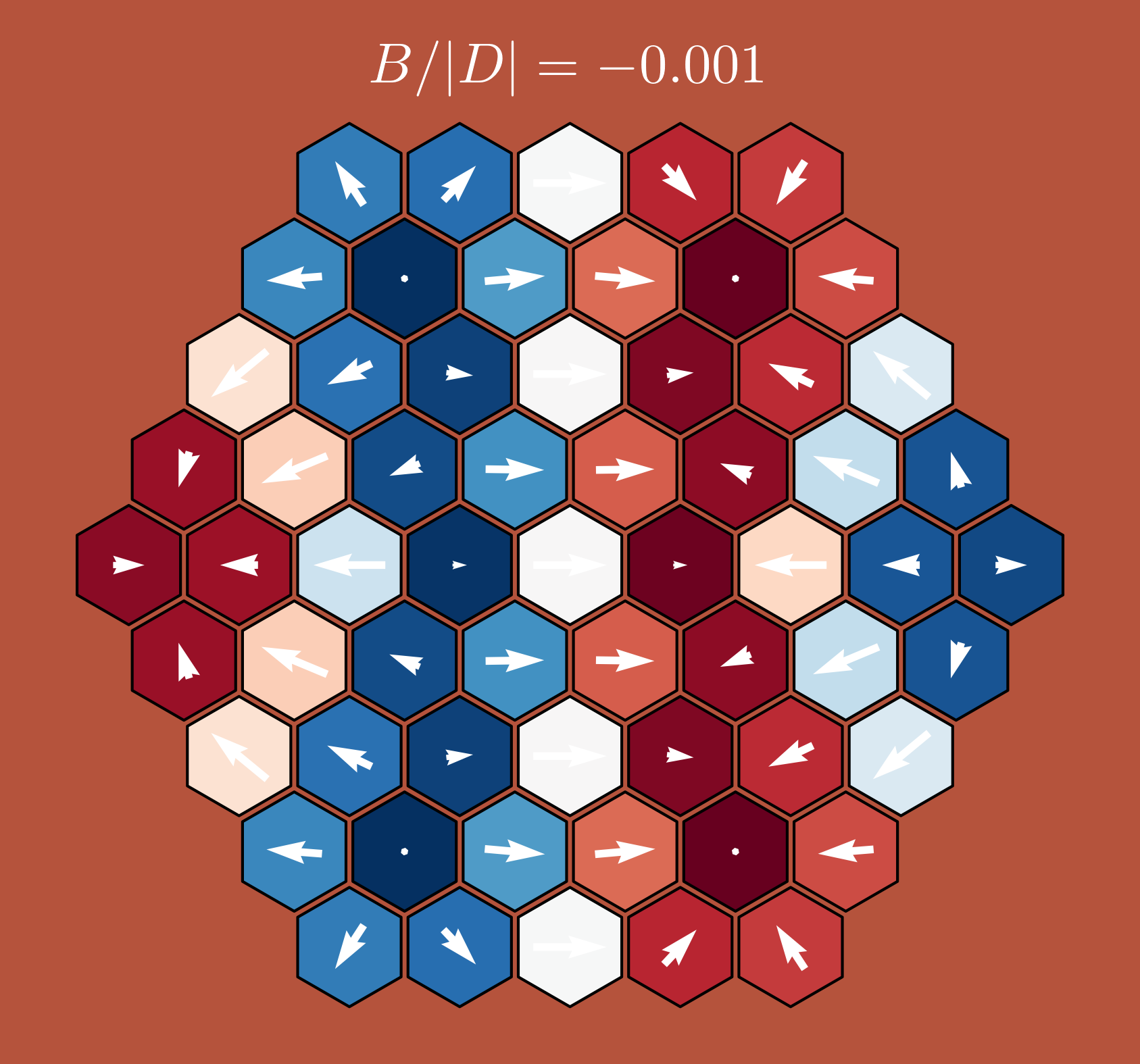
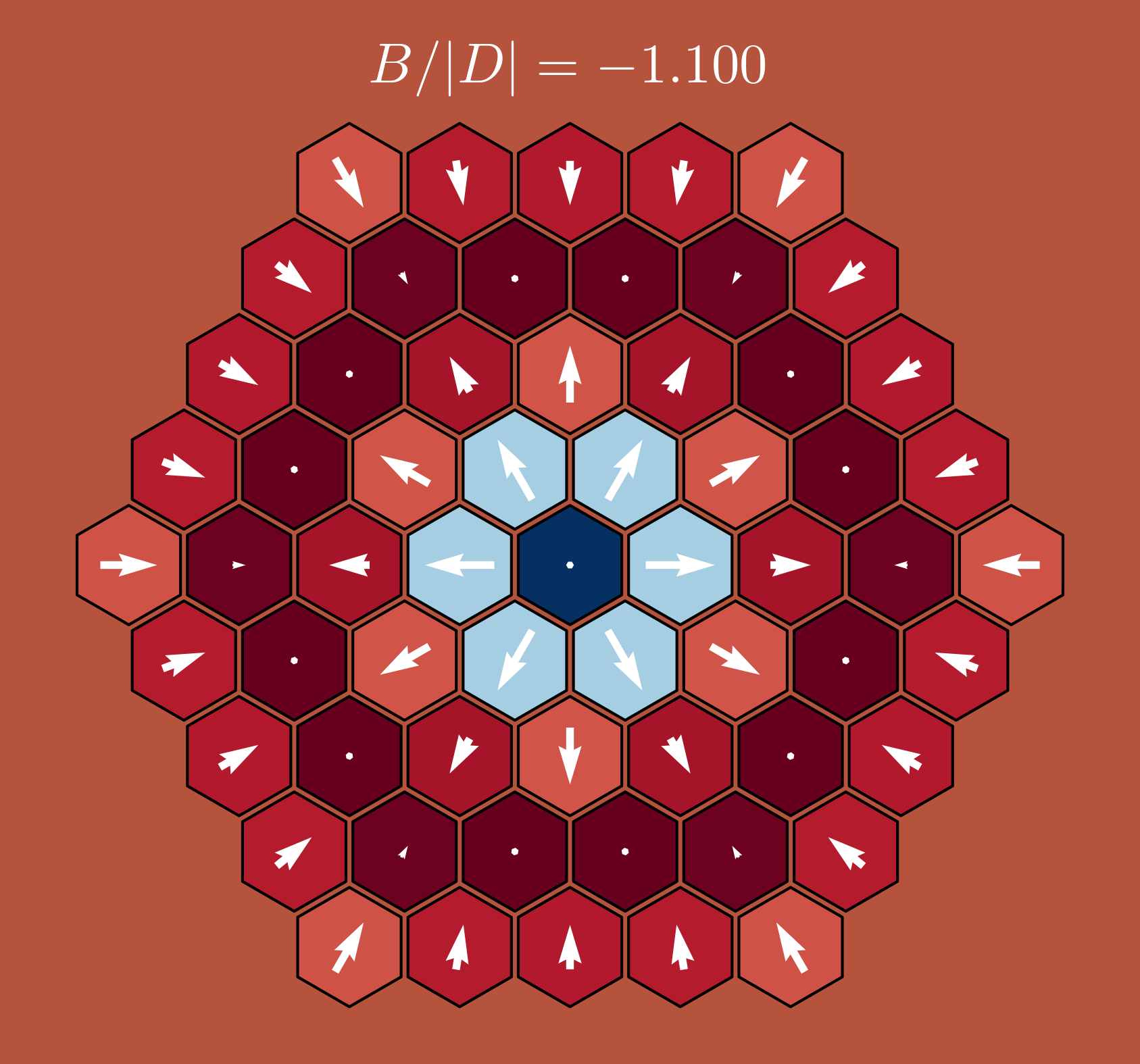

DM vs. Heisenberg vs. Zeeman
Tensor Networks
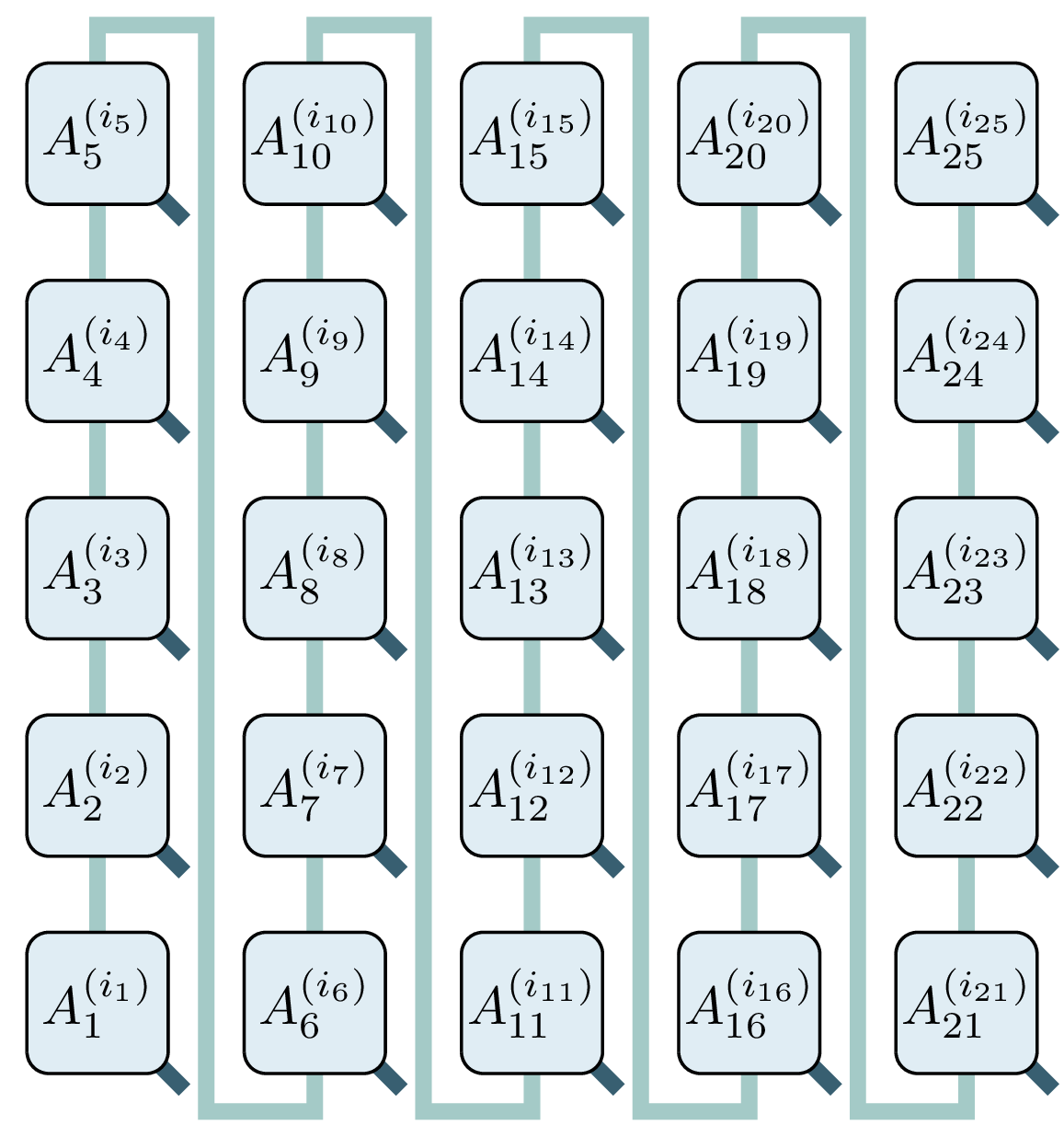
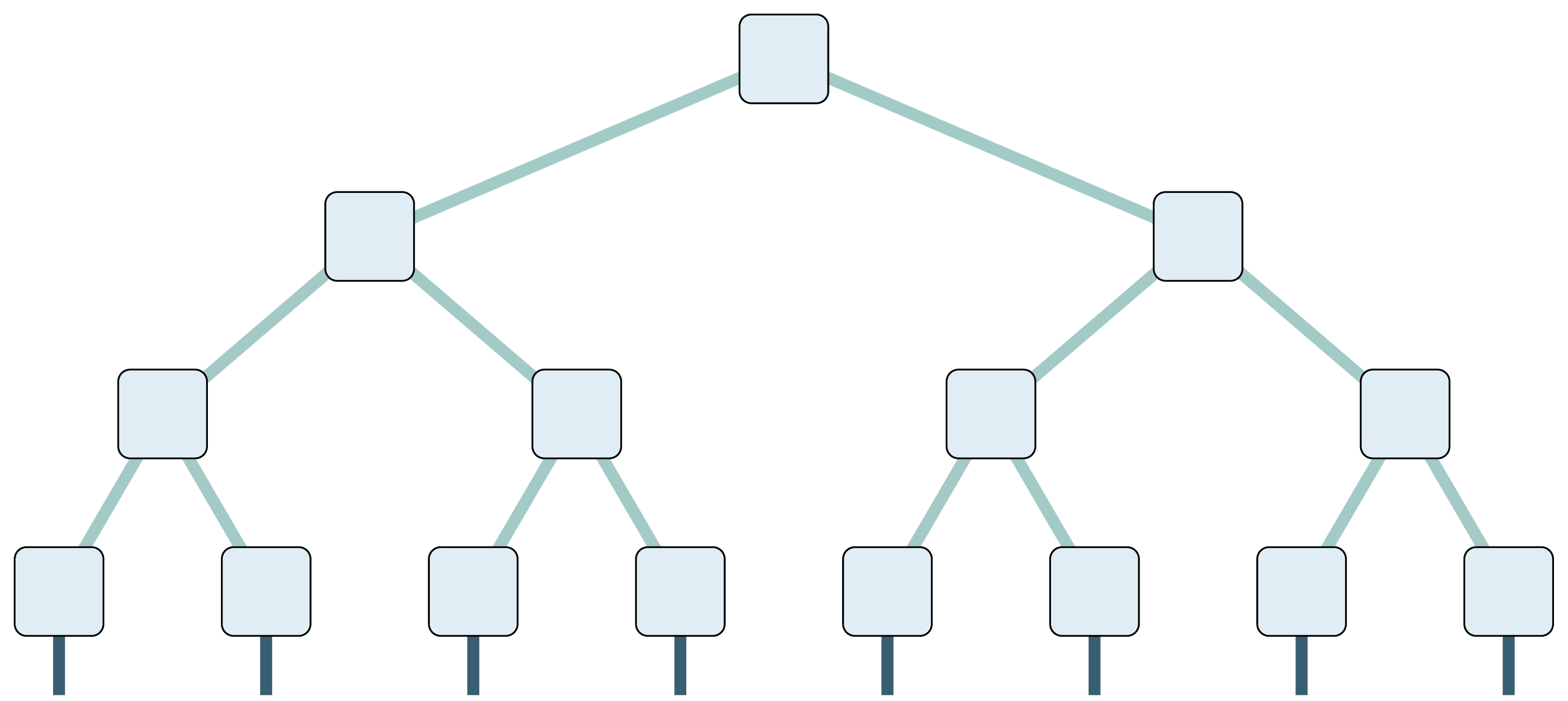
Matrix Product States (MPS)
$\psi_{i_1,i_2,...,i_N} = {\rm tr}\left(\prod_n A^{(i_n)}_{n}\right)$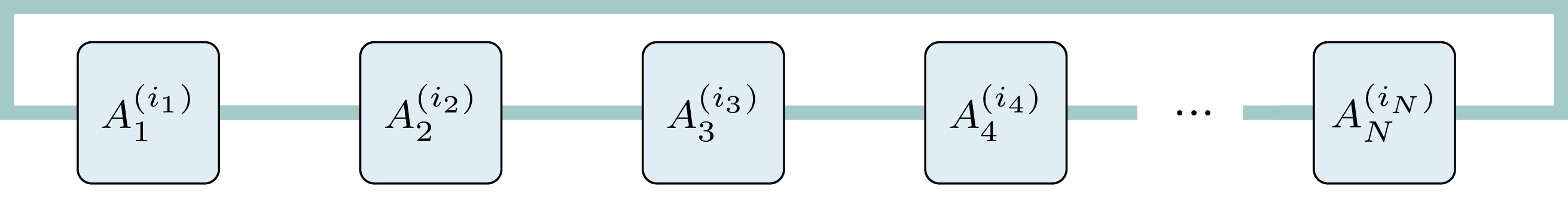
- representation of generic wavefunctions
- faithful simulation of ground and excited states
- allows investigating dynamics or open systems
Matrix Product States (MPS)
\[ \ket{\psi} = \sum_{\bm i}\psi_{i_1,i_2,...,i_N}\ket{i_1,i_2,...,i_N}\\ = \sum_{\bm i}{\rm tr}\left(\prod_n A^{(i_n)}_{n}\right)\ket{i_1,i_2,...,i_N} \]
Matrix Product States (MPS)
\[ \ket{\psi} = \sum_{\bm i}{\rm tr}\left(\prod_n A^{(i_n)}_{n}\right)\ket{i_1,i_2,...,i_N} \]
\[ \hat O = \sum_{j,j'}O_{j',j}\ket{j'}\bra{j} \]
Matrix Product States (MPS)
\[ \hat O_{q}\ket{\psi} = {\rm tr}\left(\prod_n A^{(i_n)}_{n}\right)O_{j_q',j_q}\ket{j_q'}\braket{j_q|i_1,i_2,...,i_N}\\ = {\rm tr}\left(\prod_n A^{(i_n)}_{n}\right)O_{j_q',i_q}\ket{i_1,i_2,...,j_q',...,i_N} \]
- operators change the wavefunction
- operators transform the MPS matrices
Matrix Product States (MPS)
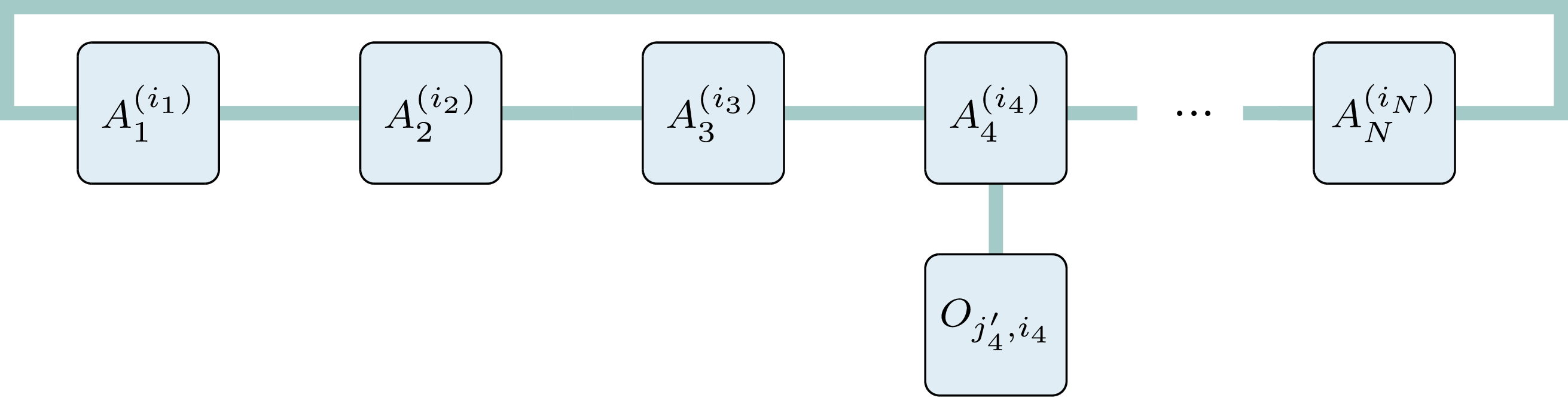
- operators transform the MPS matrices
- leads to matrix product operators (MPO)
- efficient computation of the MPS energy
Matrix Product States (MPS)
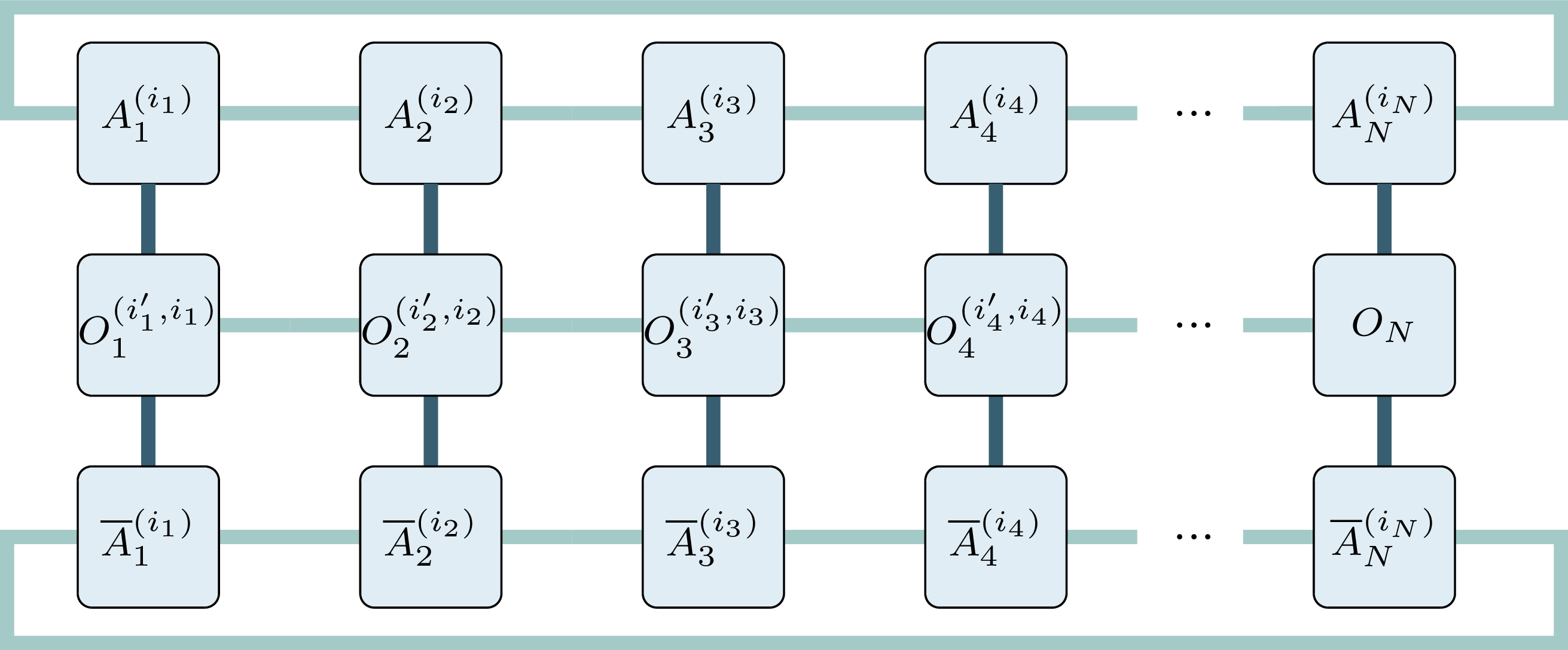
- operators transform the MPS matrices
- leads to matrix product operators (MPO)
- efficient computation of the MPS energy
Density matrix renormalization group

- variational principle $ E_{\rm GS} = \min_{\psi}\braket{\psi|H|\psi} $
- $ \mathcal L = \braket{\psi|H|\psi} - \lambda(\braket{\psi|\psi}-1) $
- solve the equations of motion for each tensor $A^{(i_n)}_n$
Density matrix renormalization group

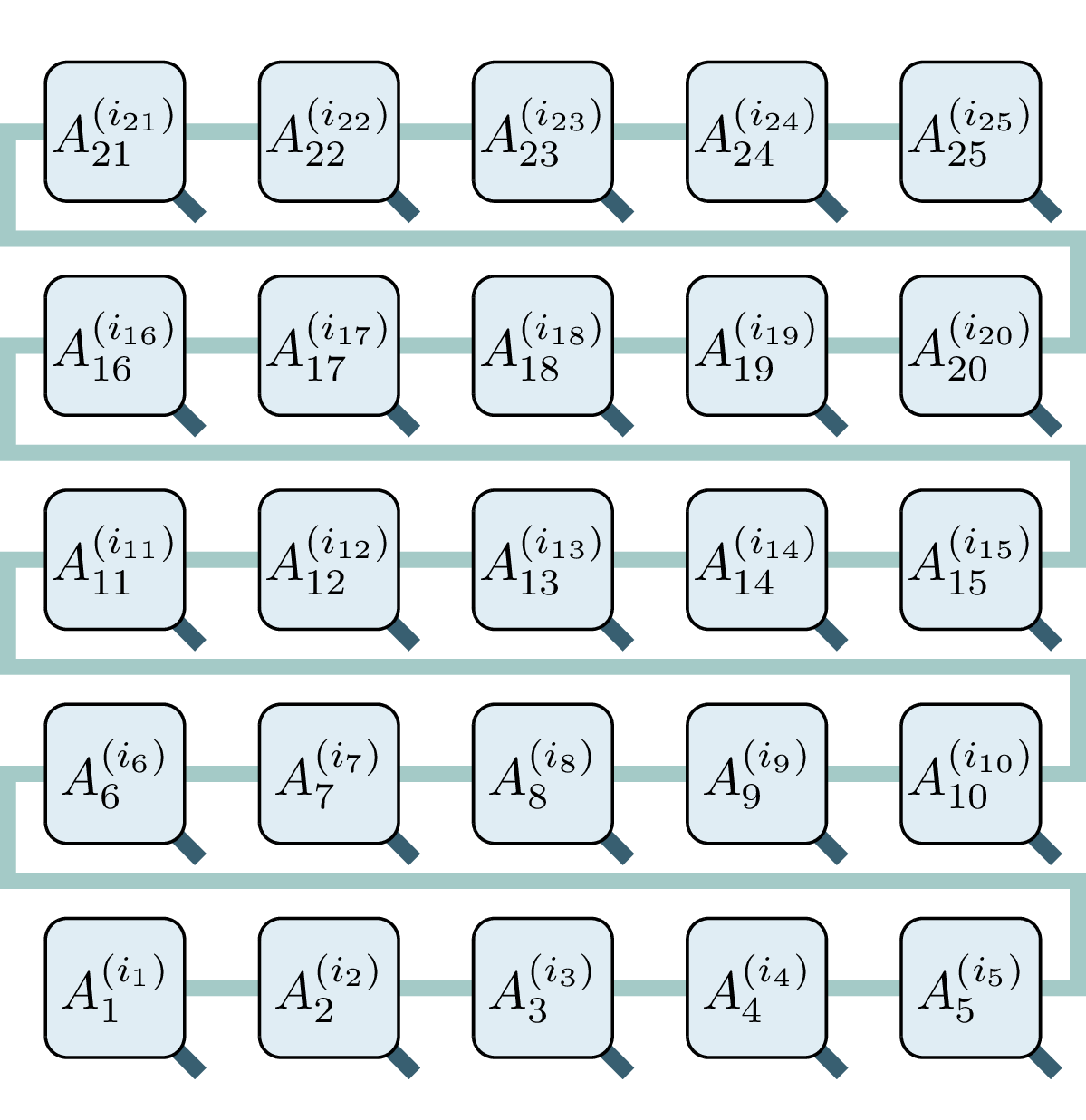
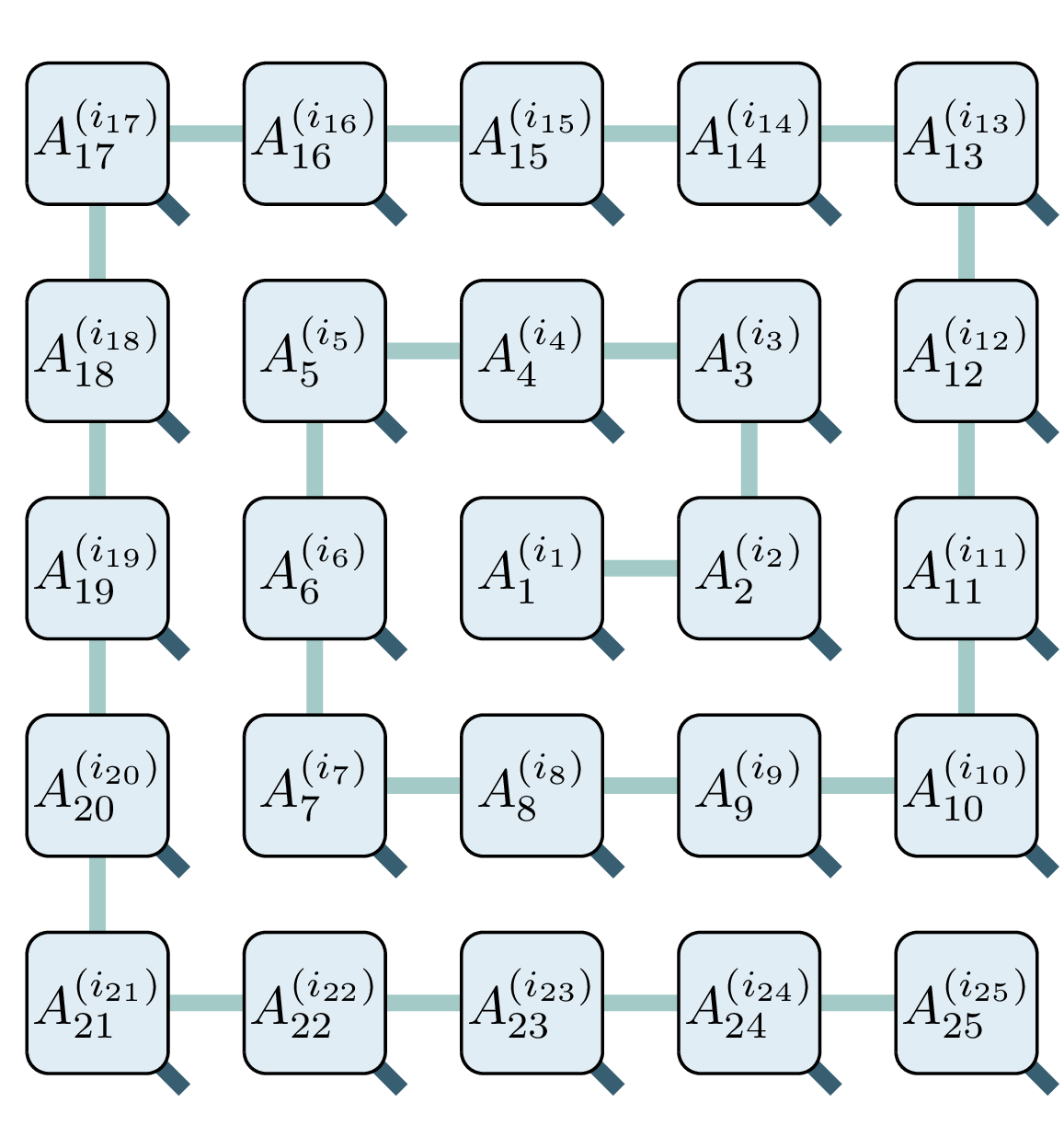
- map 2D system to 1D
- perform DMRG in time $T\propto\mathcal O(M^3)$
- measure observables
Quantum Spin $1/2$ Model
\[ \rlap{$E$}\phantom{\hat H} = \overbrace{ J \sum_{\bm r, \bm r'} \bm S_{\bm r}\cdot\bm S_{\bm r'} }^{\rm Heisenberg} + \overbrace{ \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\bm S_{\bm r_i}\times\bm S_{\bm r_j} }^{\rm Dzyaloshinskii-Moriya} \\ \underbrace{ +\sum_{\bm r}\bm B_{\bm r}\cdot\bm S_{\bm r} }_{\rm external\ Zeeman\ Field} \quad \phantom{ \underbrace{ + K \sum_{\bm r}\hat{S}_{z,\bm r}\hat{S}_{z,\bm r} }_{\rm uniaxial\ anisotropy} } \]Quantum Spin $1/2$ Model
\[ \hat H = \overbrace{ J \sum_{\bm r, \bm r'} \hat{\bm S}_{\bm r}\cdot\hat{\bm S}_{\bm r'} }^{\rm Heisenberg} + \overbrace{ \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\hat{\bm S}_{\bm r_i}\times\hat{\bm S}_{\bm r_j} }^{\rm Dzyaloshinskii-Moriya} \\ \underbrace{ +\sum_{\bm r}\bm B_{\bm r}\cdot\hat{\bm S}_{\bm r} }_{\rm external\ Zeeman\ Field} \phantom{ \quad \underbrace{ + K \sum_{\bm r}\hat{S}_{z,\bm r}\hat{S}_{z,\bm r} }_{\rm uniaxial\ anisotropy} } \]Quantum Spin $1/2$ Model
\[ \hat H = \overbrace{ J \sum_{\bm r, \bm r'} \hat{\bm S}_{\bm r}\cdot\hat{\bm S}_{\bm r'} }^{\rm Heisenberg} + \overbrace{ \sum_{\braket{i,j}} \bm D_{\bm r_i,\bm r_j}\cdot\hat{\bm S}_{\bm r_i}\times\hat{\bm S}_{\bm r_j} }^{\rm Dzyaloshinskii-Moriya} \\ \underbrace{ +\sum_{\bm r}\bm B_{\bm r}\cdot\hat{\bm S}_{\bm r} }_{\rm external\ Zeeman\ Field} \quad \underbrace{ + K \sum_{\bm r}\hat{S}_{z,\bm r}\hat{S}_{z,\bm r} }_{\rm uniaxial\ anisotropy} \]Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$

Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$

Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
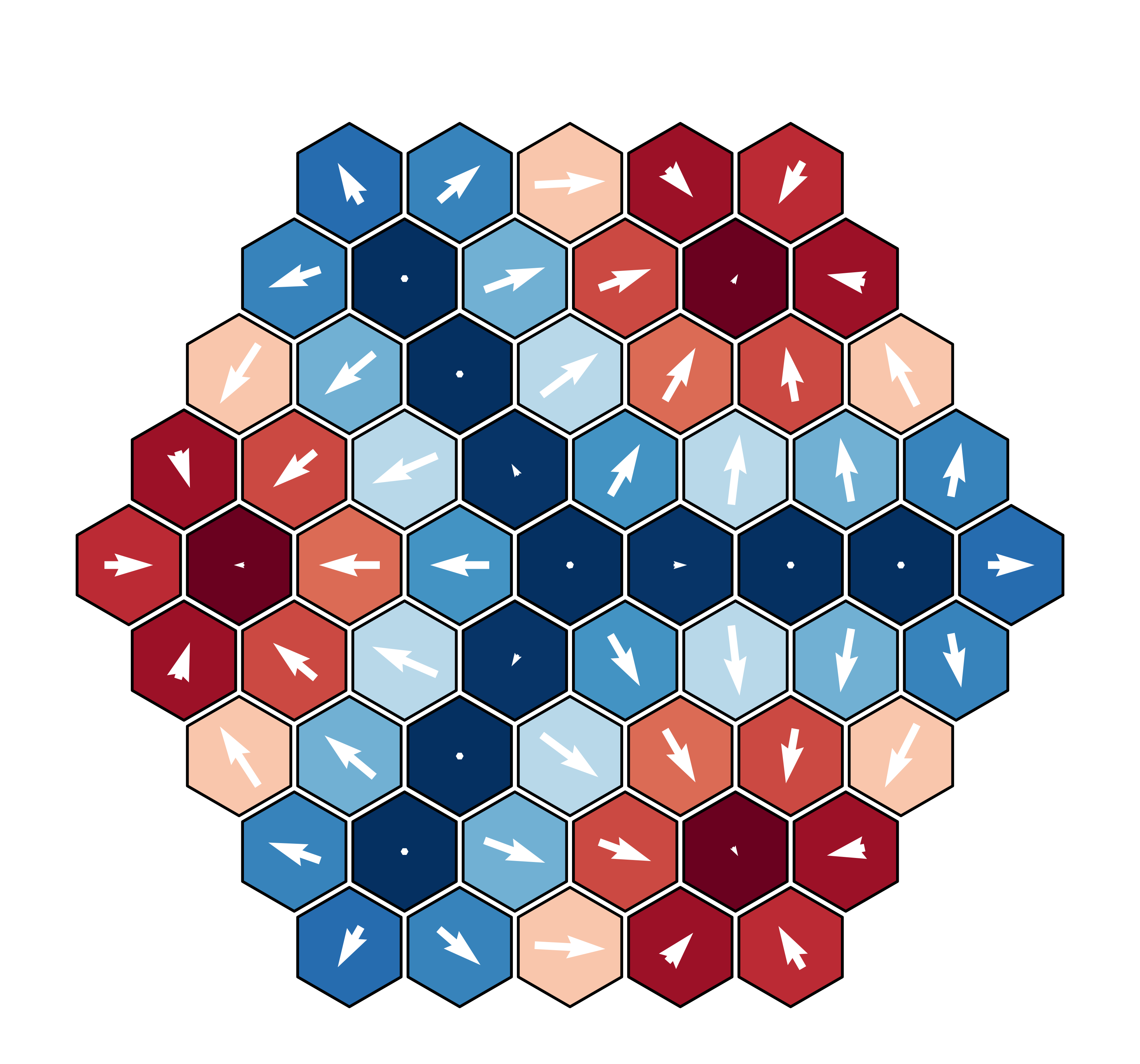
 $B = -0.1|D|$
$B = -0.1|D|$
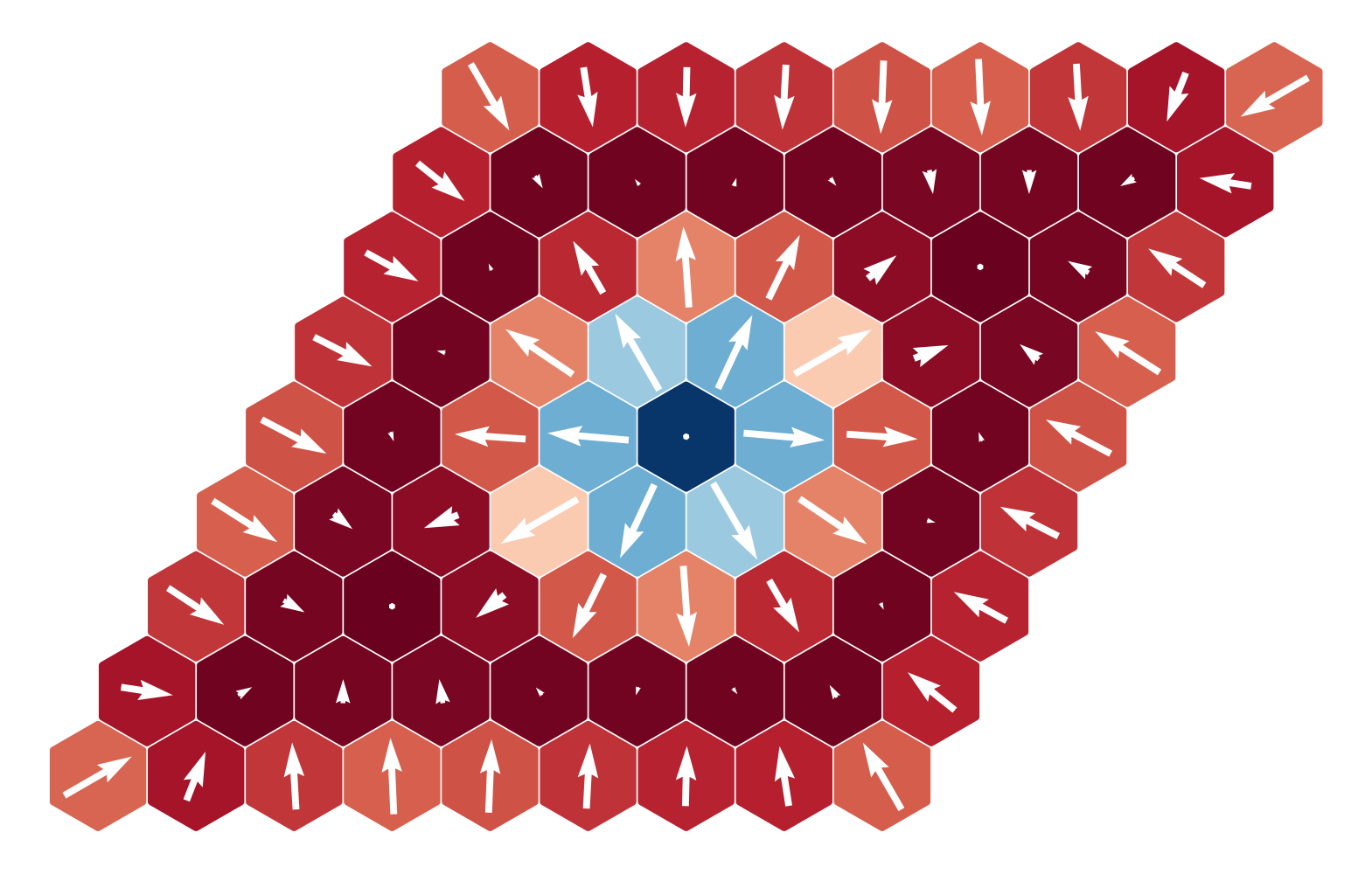 $B = -0.5|D|$
$B = -0.5|D|$
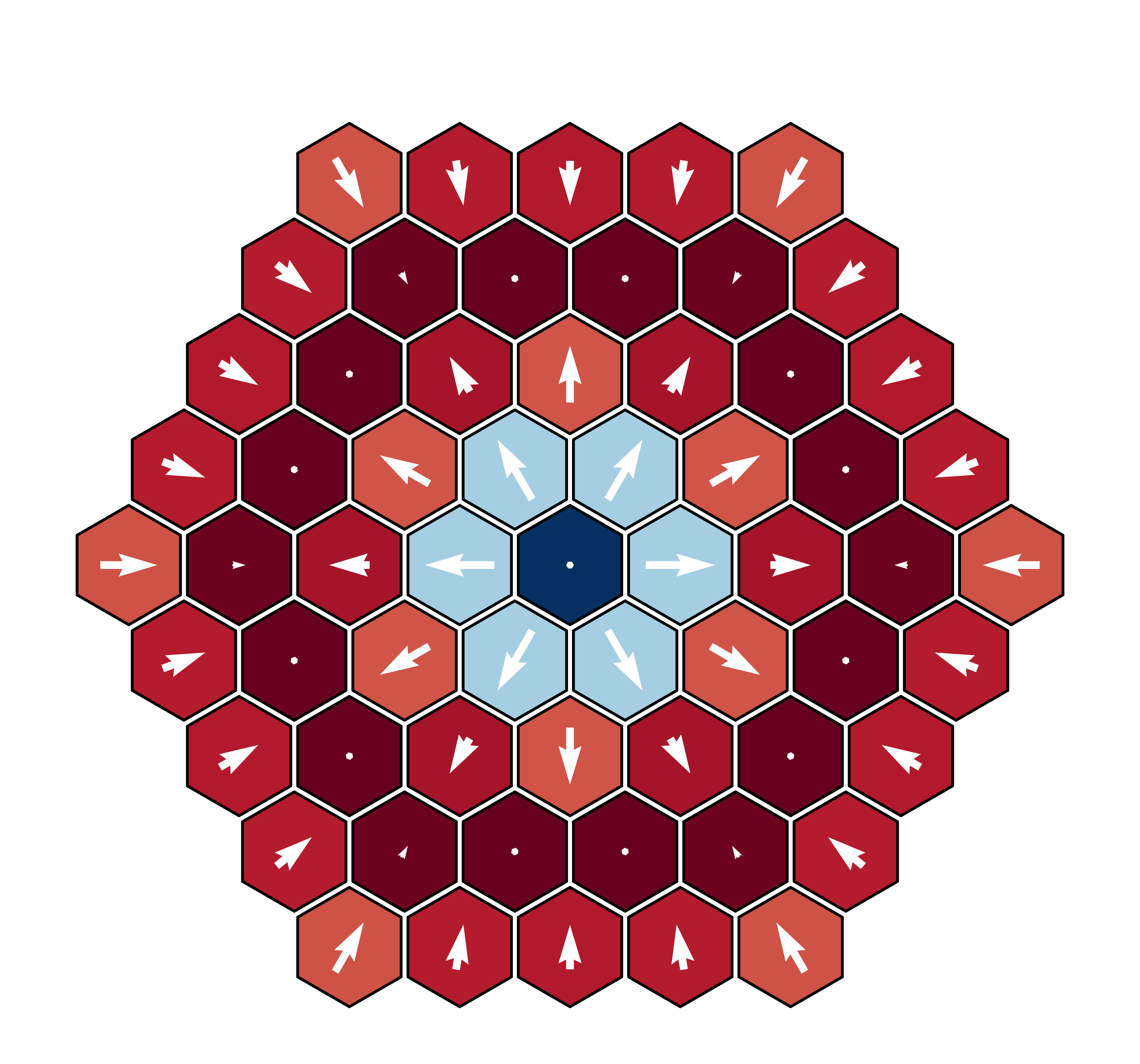
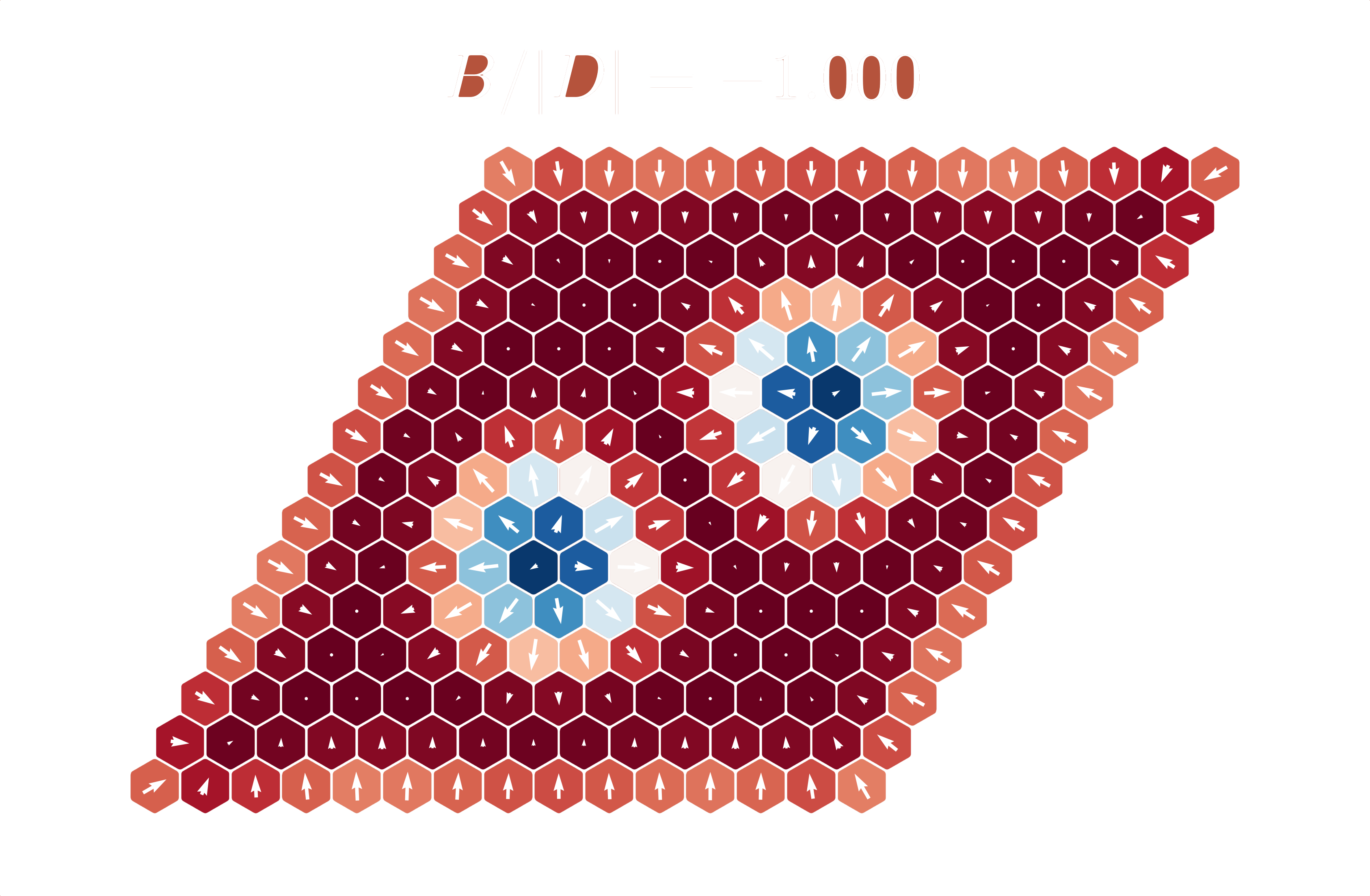
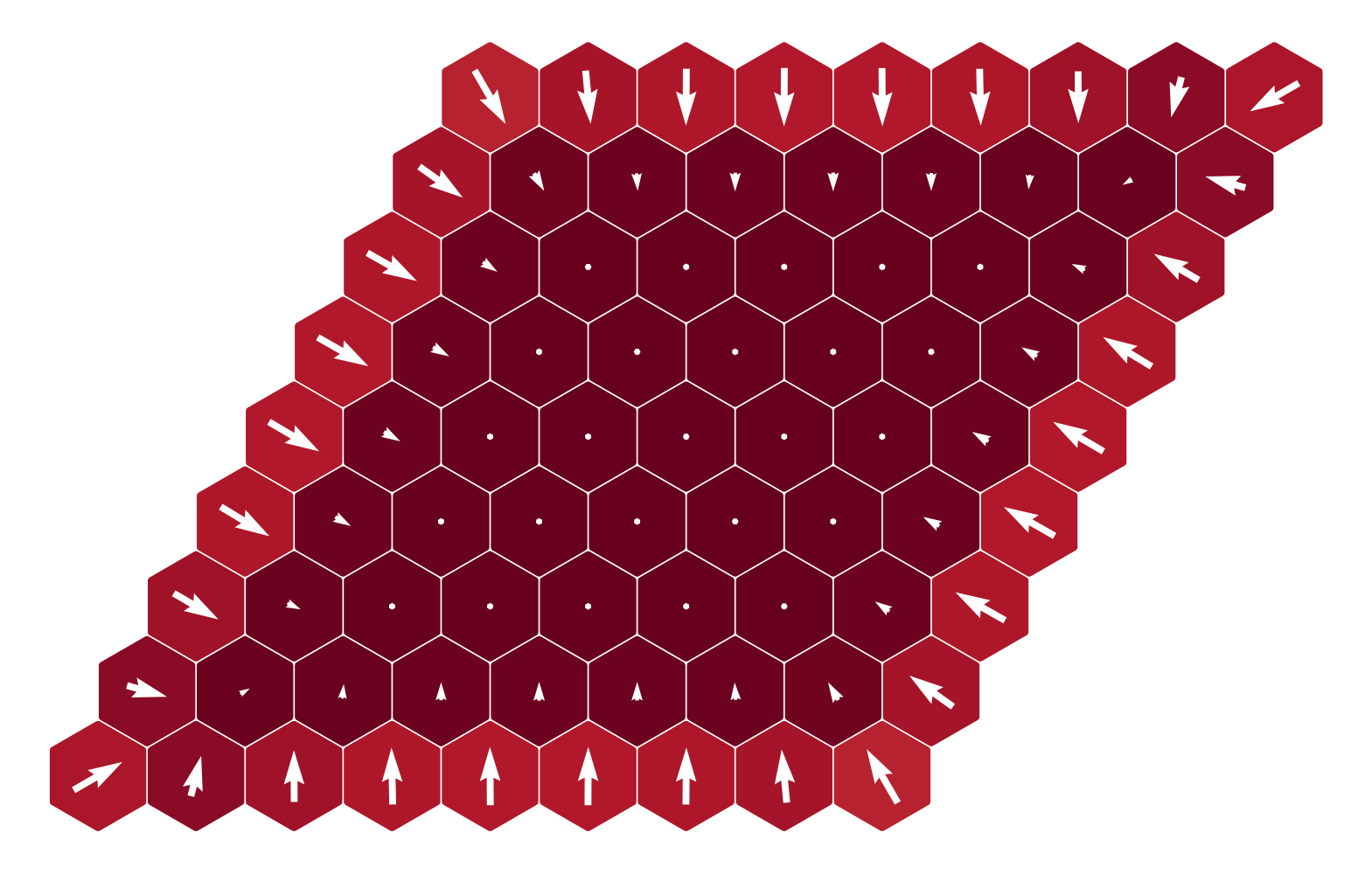 $B = -1.0|D|$
$B = -1.0|D|$
Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
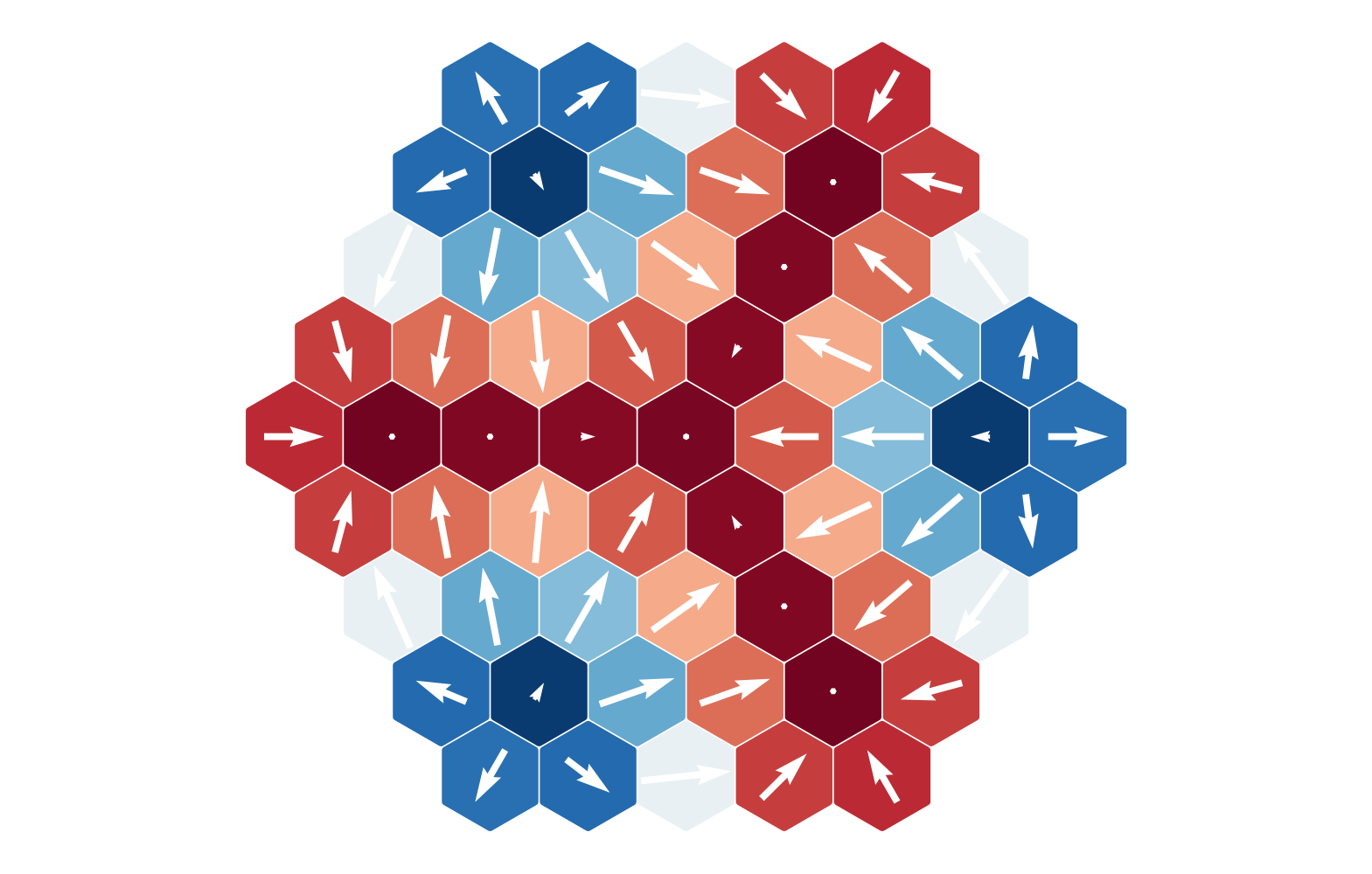 $B = -0.1|D|$
$B = -0.1|D|$
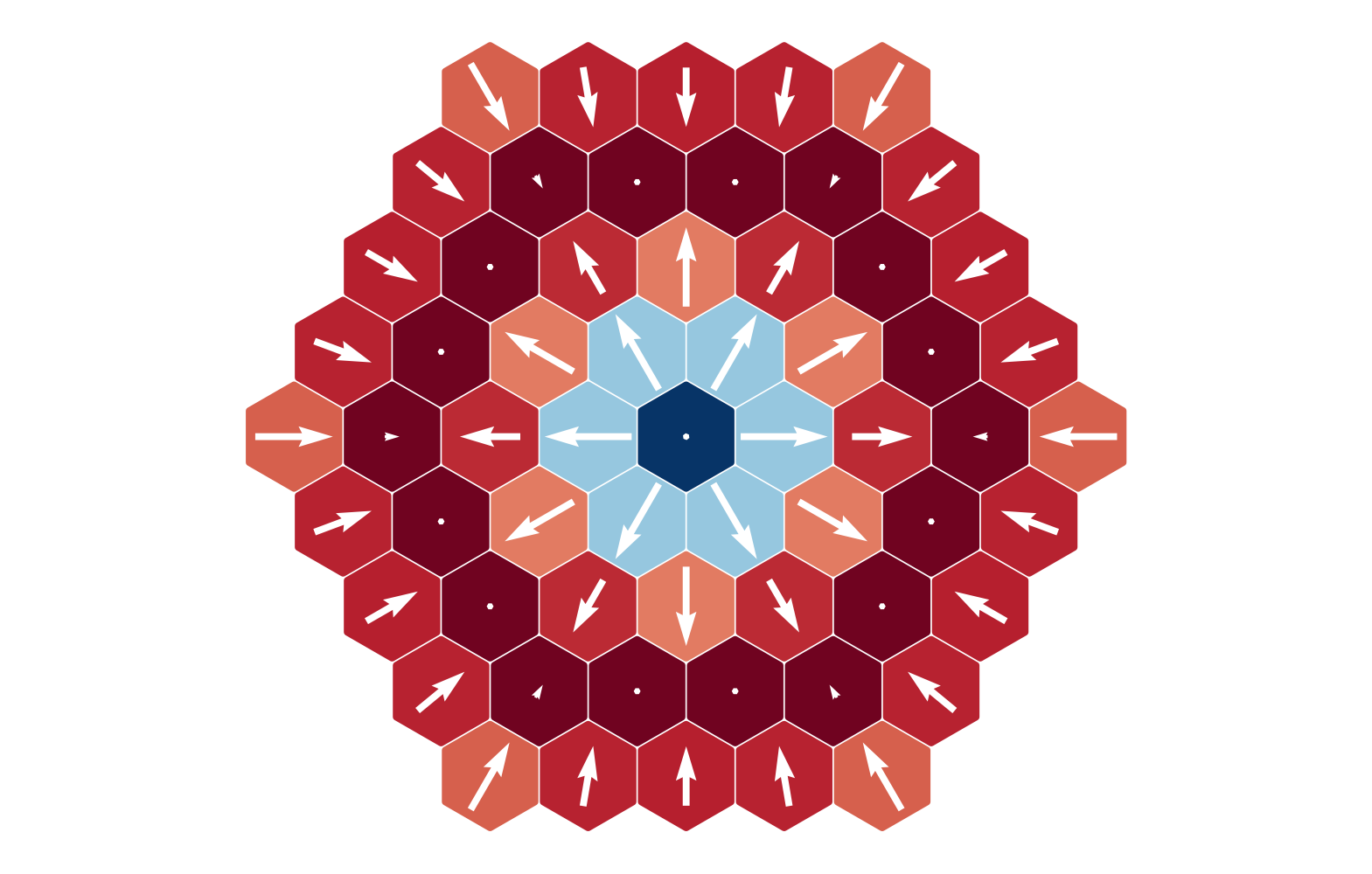 $B = -0.5|D|$
$B = -0.5|D|$
 $B = -1.0|D|$
$B = -1.0|D|$
Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
 $B = -0.1|D|$
$B = -0.1|D|$
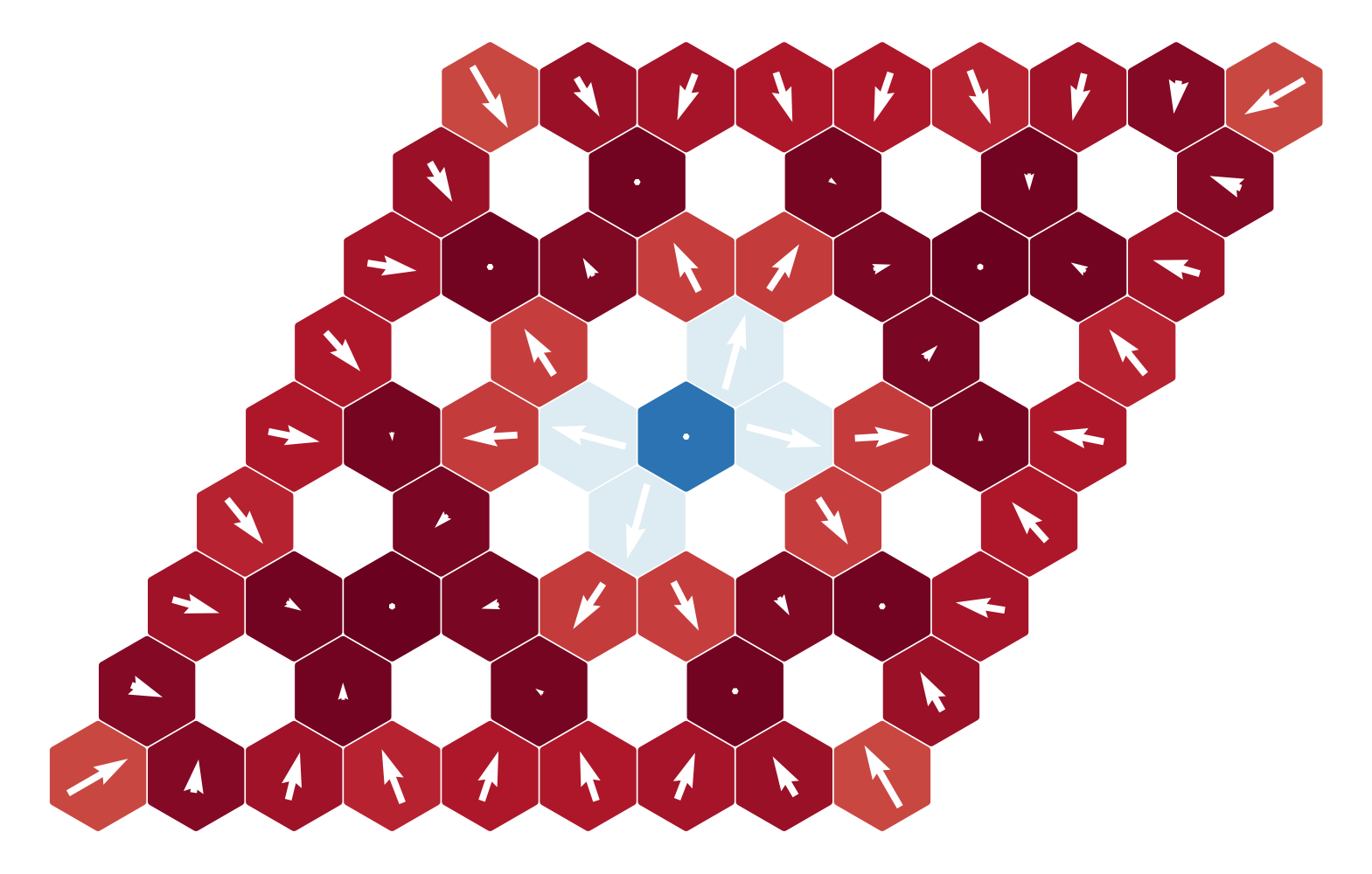 $B = -0.5|D|$
$B = -0.5|D|$
 $B = -1.0|D|$
$B = -1.0|D|$
Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
 $B = -0.1|D|$
$B = -0.1|D|$
 $B = -0.5|D|$
$B = -0.5|D|$
 $B = -1.0|D|$
$B = -1.0|D|$
Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
 $B = -0.1|D|$
$B = -0.1|D|$
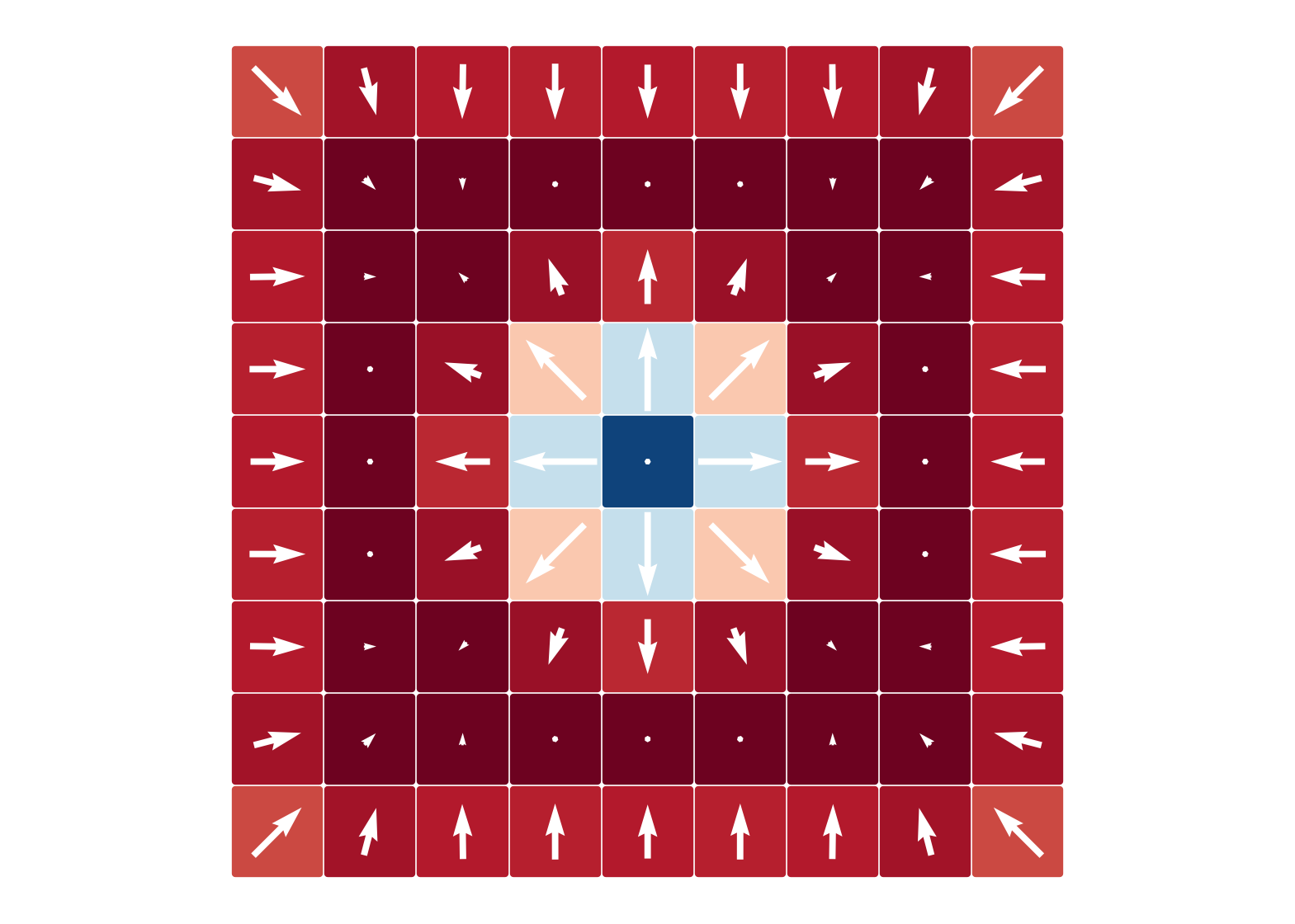 $B = -0.5|D|$
$B = -0.5|D|$
 $B = -1.0|D|$
$B = -1.0|D|$
Quantum Spin Model
fix $J/|D|=-0.5$, ground states for varying $B/|D|$
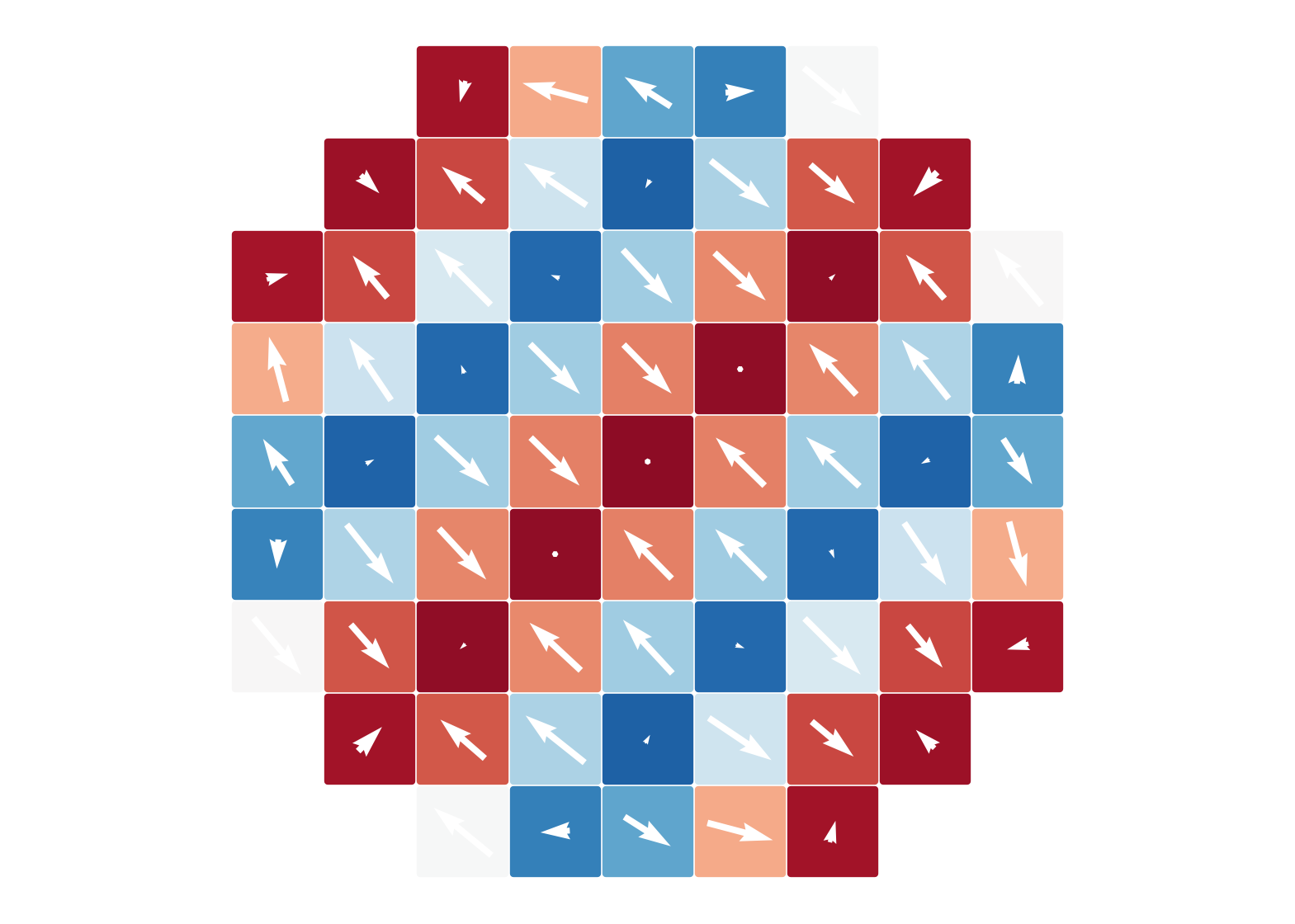 $B = -0.1|D|$
$B = -0.1|D|$
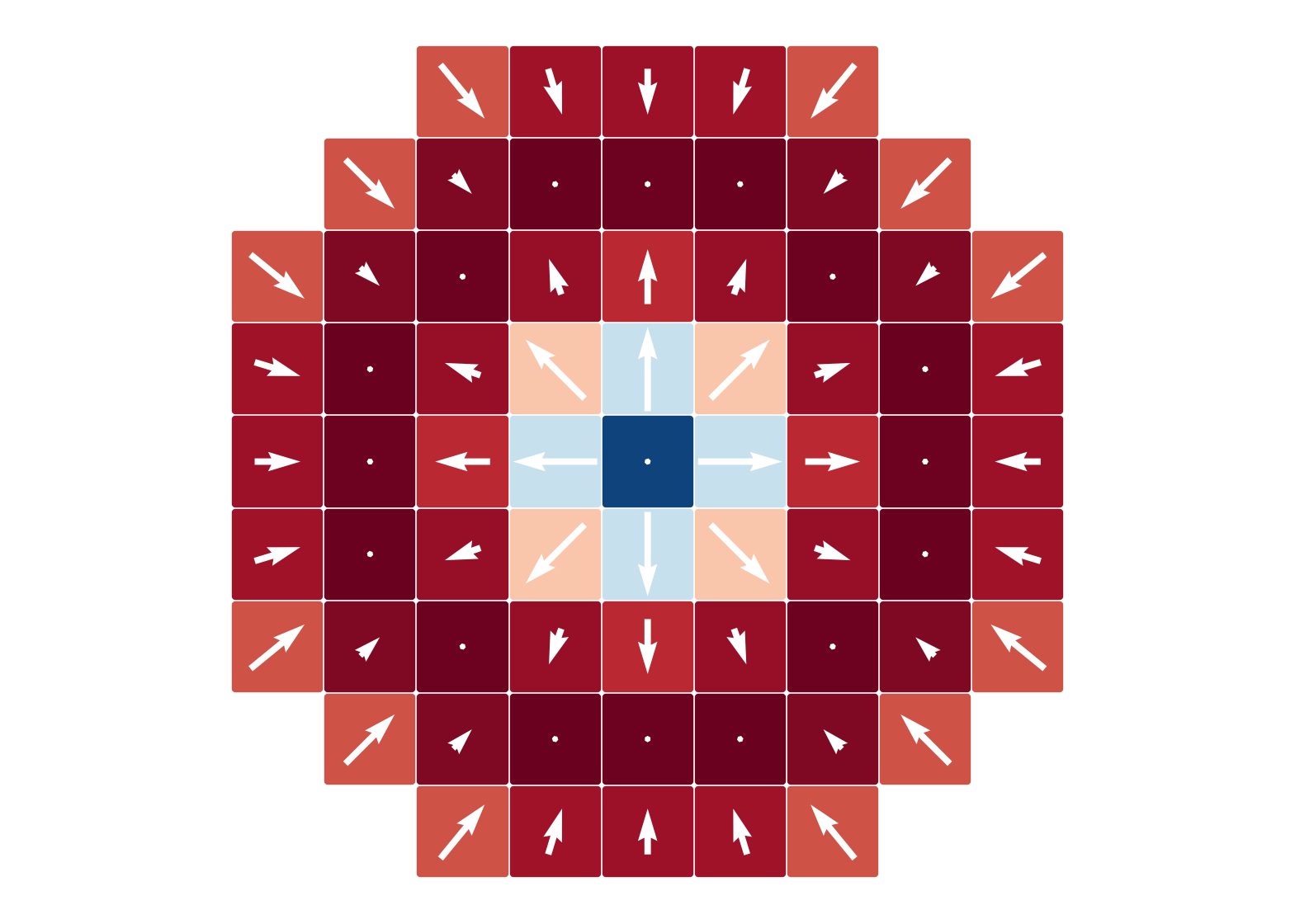 $B = -0.5|D|$
$B = -0.5|D|$
 $B = -1.0|D|$
$B = -1.0|D|$
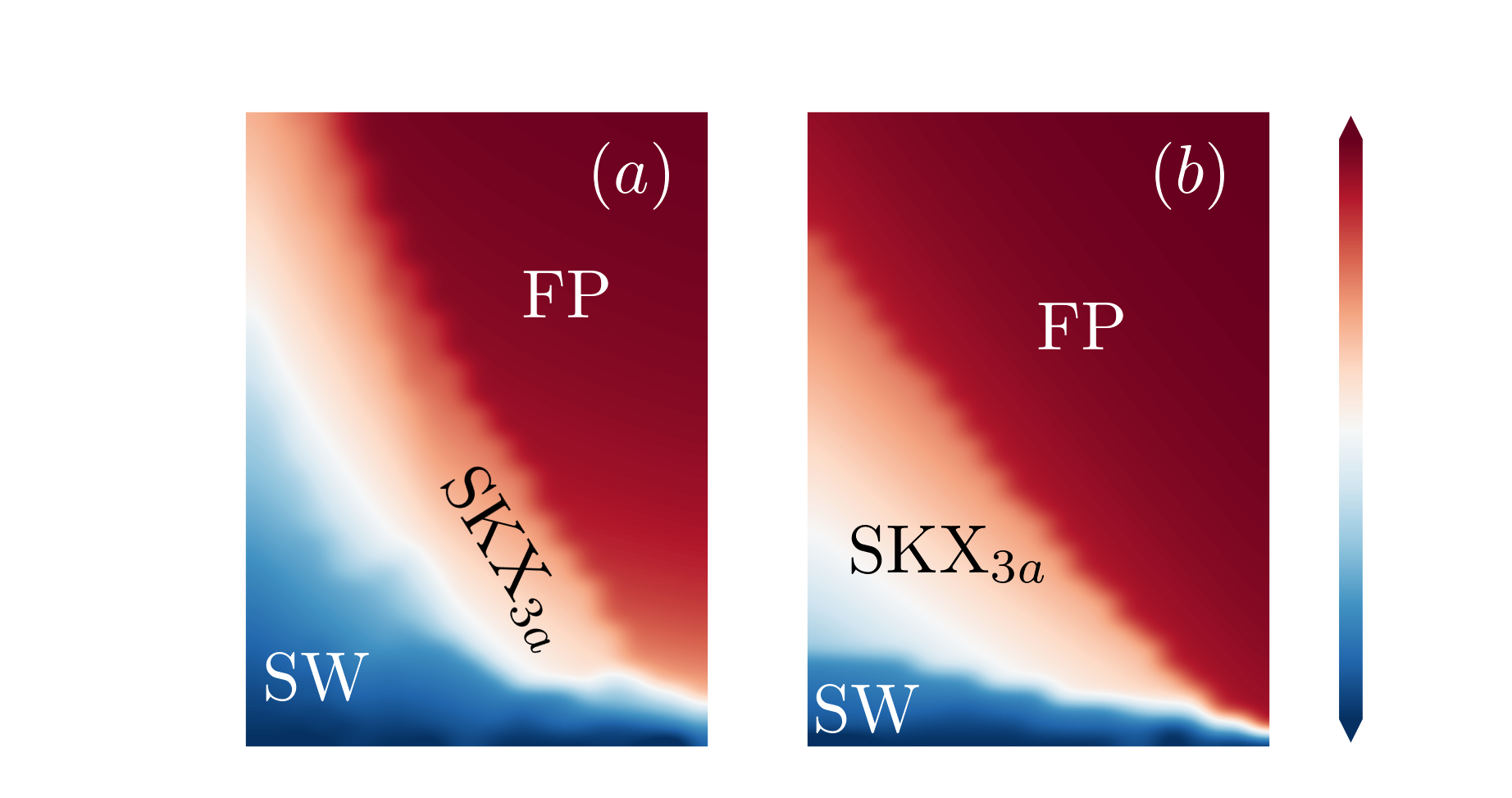
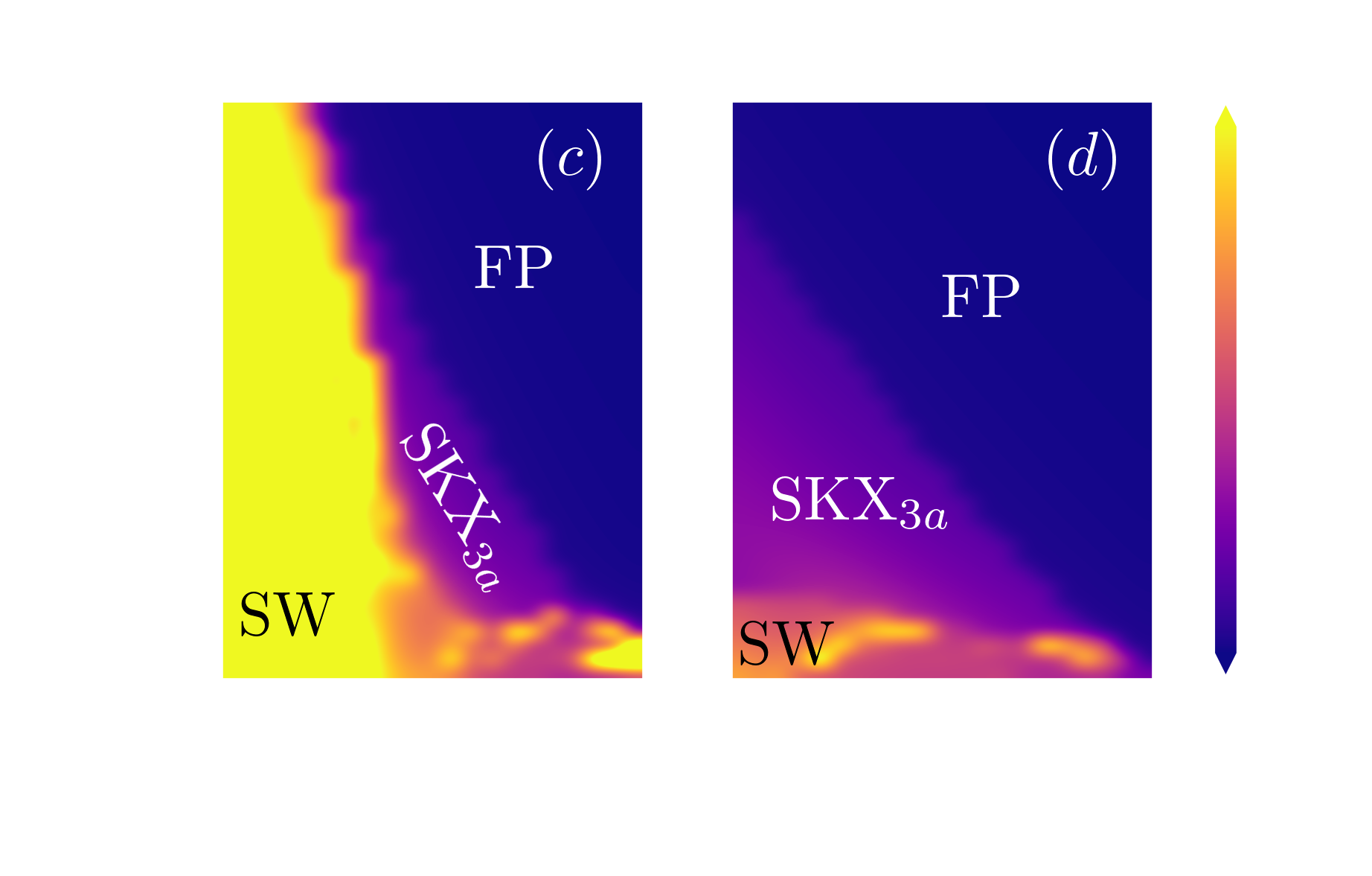
Quantum Spin Model
norm of the spin expectation value

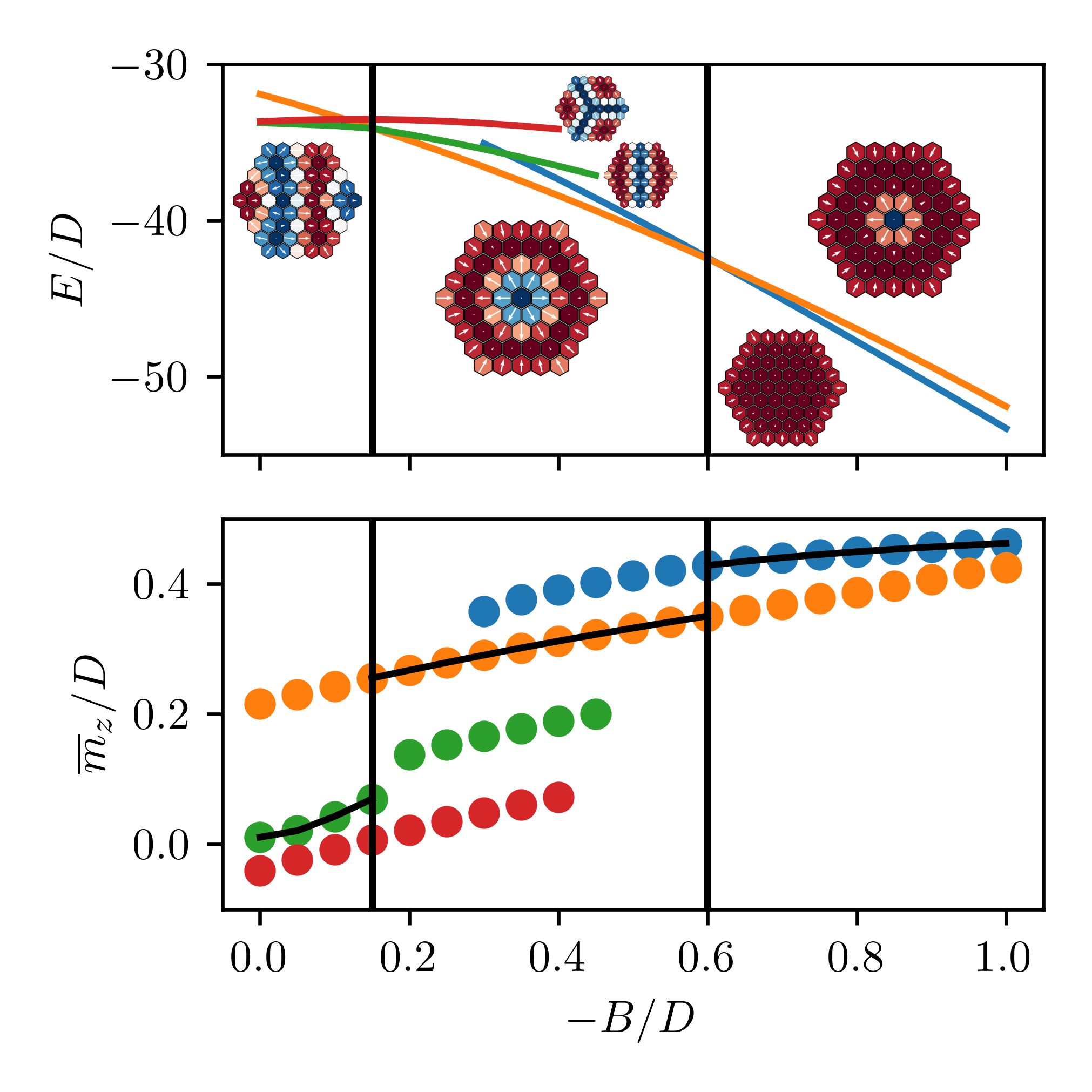
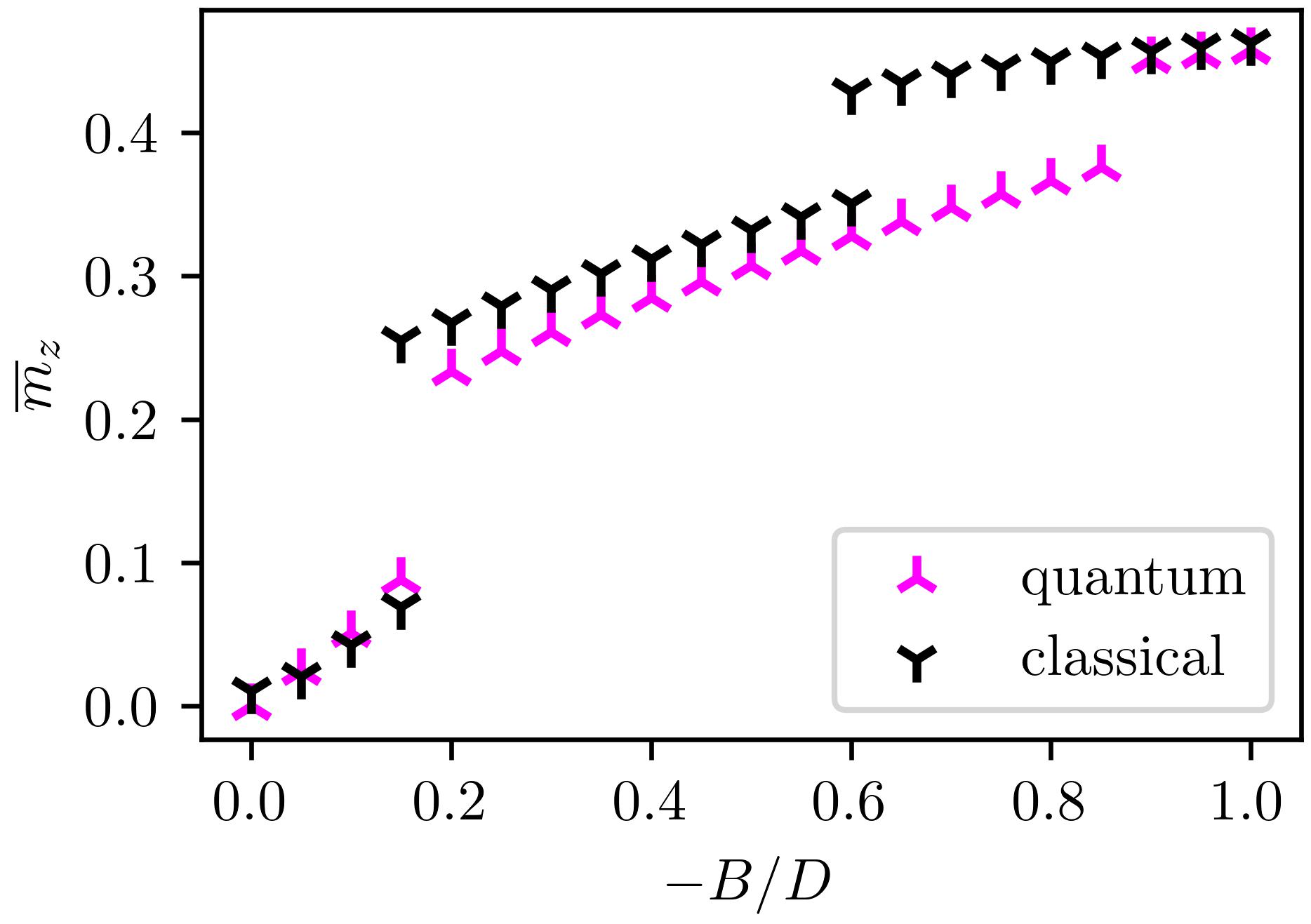
Quantum Spin Model
average magnetization and entanglement entropy



Quantum Spin Model
$J=-0.5|D|$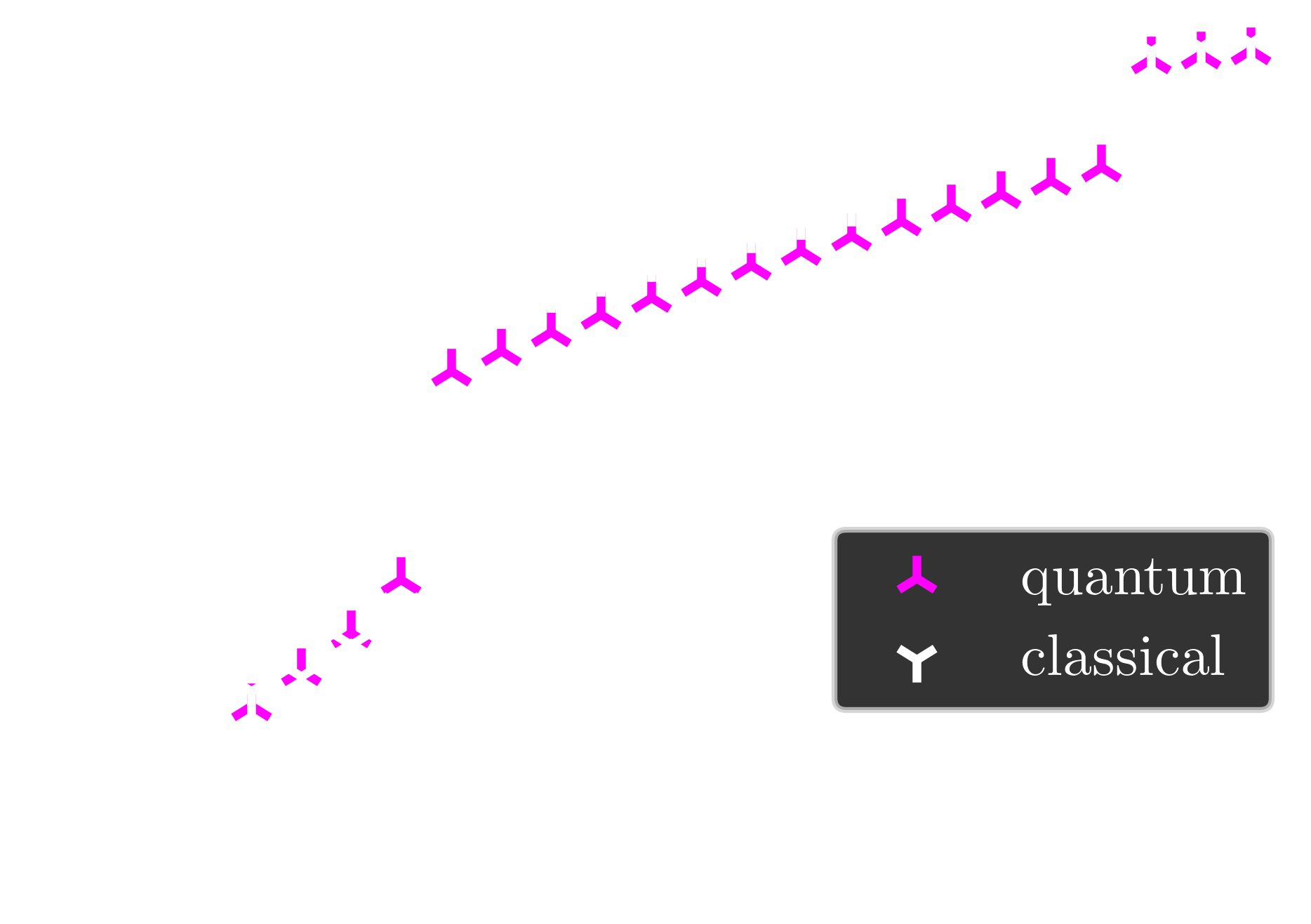
quantum Skyrmion phase more robust against $B$
Quantum Spin Model
For spin $s=1/2$: quantum skyrmion lattices

Quantum Spin Model
For spin $s=1/2$: quantum skyrmion lattices

Quantum Spin Model
For spin $s=1/2$: quantum skyrmion lattices

Quantum Spin Model
For spin $s=1/2$: quantum skyrmion lattices

Quantum Spin Model
Concurrence: measure for pair entanglement
Quantum Spin Model
Concurrence: measure for pair entanglement
Quantum Spin Model
Concurrence: measure for pair entanglement
\[ C_{\bm r_1, \bm r_2} = {\rm max}\left\{0, \lambda_1-\lambda_2-\lambda_3-\lambda_4 \right\}\\ \lambda_i > \lambda_{i+1},\ \lambda\in\sigma(R_{\bm r_1, \bm r_2}) \] \[ R_{\bm r_1, \bm r_2} = (\sigma_y\otimes\sigma_y)\rho^*_{\bm r_1,\bm r_2}(\sigma_y\otimes\sigma_y)\\ \rho_{\bm r_1, \bm r_2,\alpha,\beta} = \braket{\hat \sigma_{\bm r_1}^\alpha\hat \sigma_{\bm r_1}^\beta} \]Quantum Spin Model
Concurrence: measure for pair entanglement
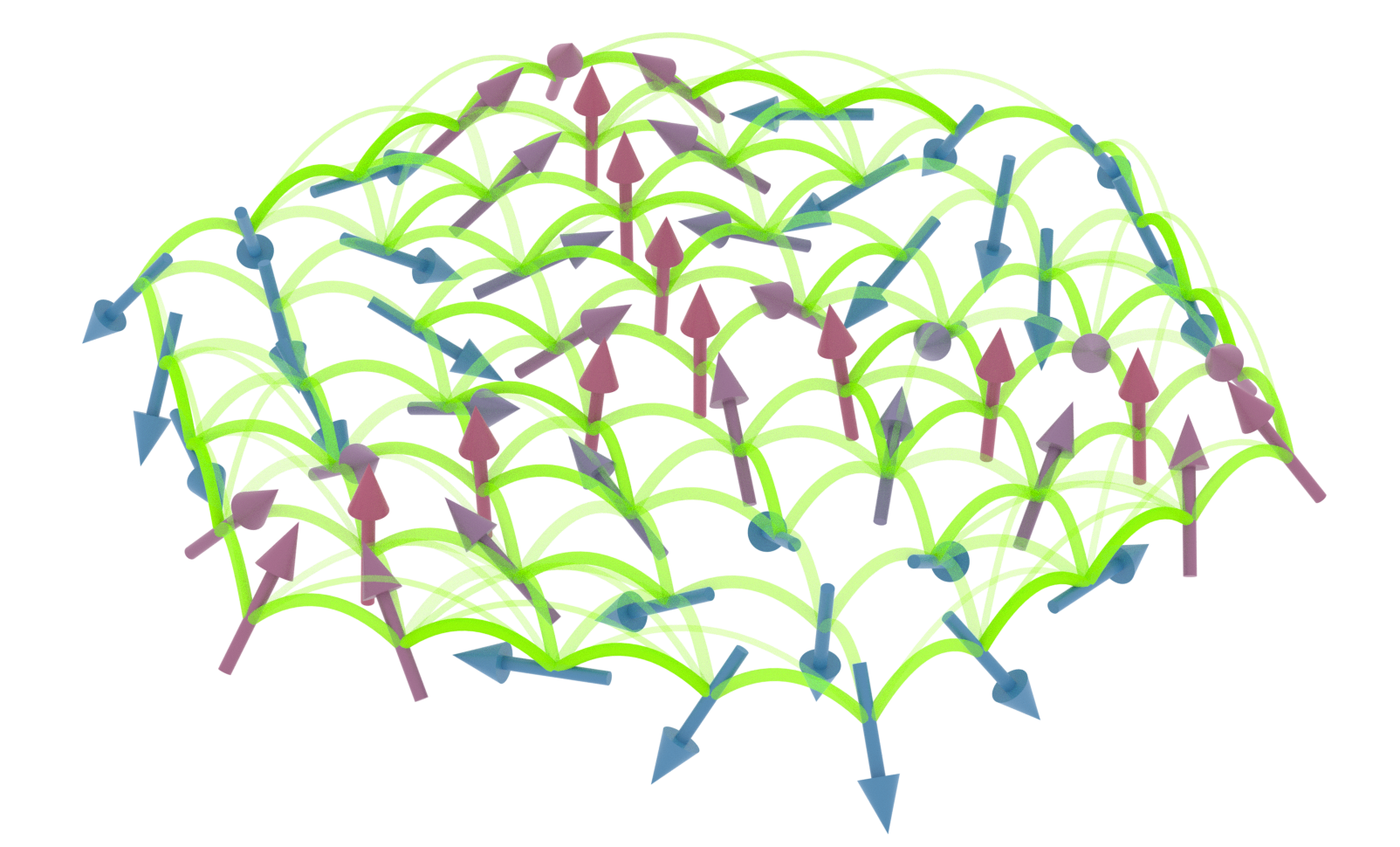 $B=-0.1|D|$
$B=-0.1|D|$
 $B=-0.5|D|$
$B=-0.5|D|$
 $B=-1.0|D|$
$B=-1.0|D|$
Quantum Spin Model
Concurrence: measure for pair entanglement

Quantum Spin Model
Concurrence: measure for pair entanglement
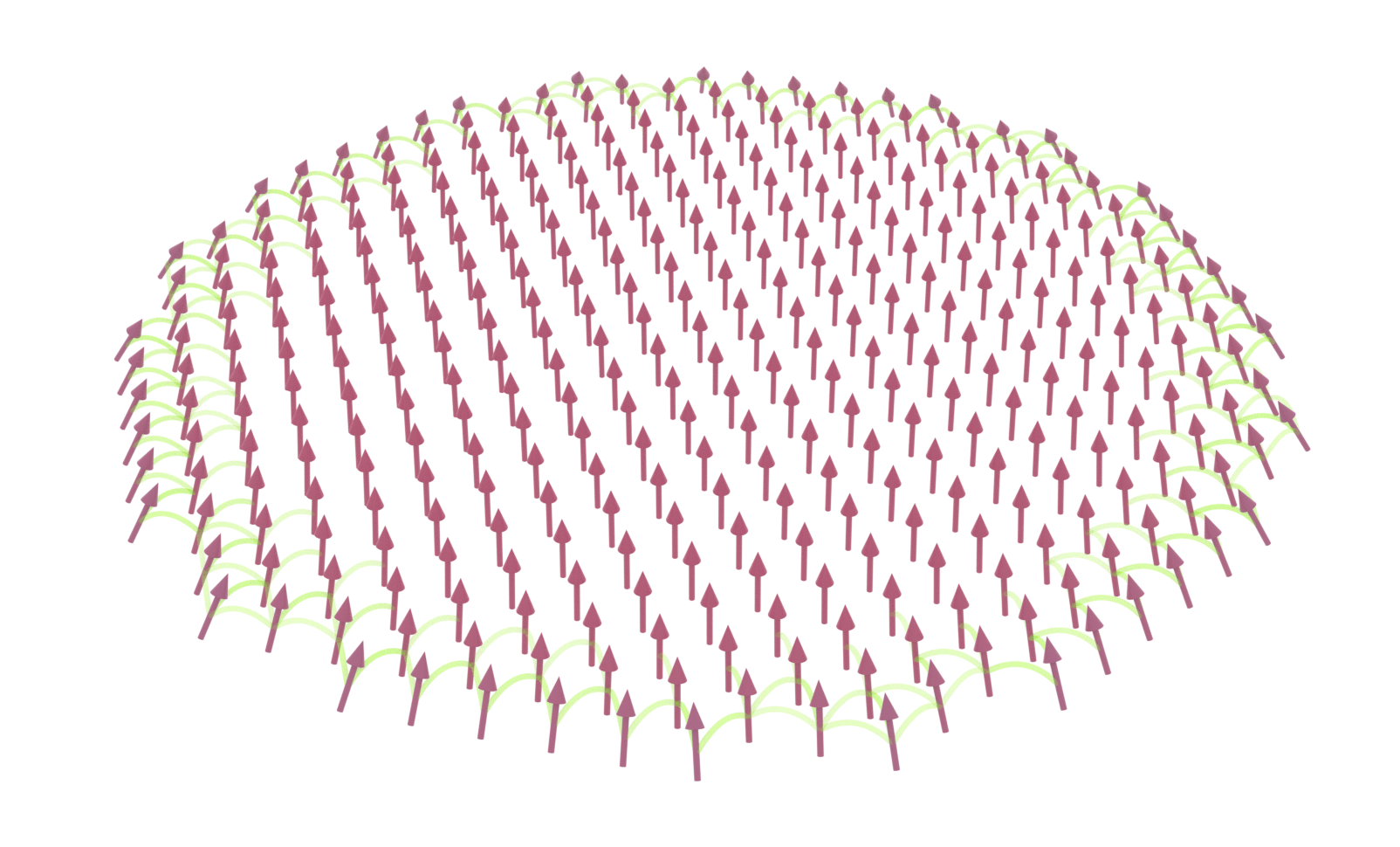
Quantum Spin Model
Concurrence: measure for pair entanglement
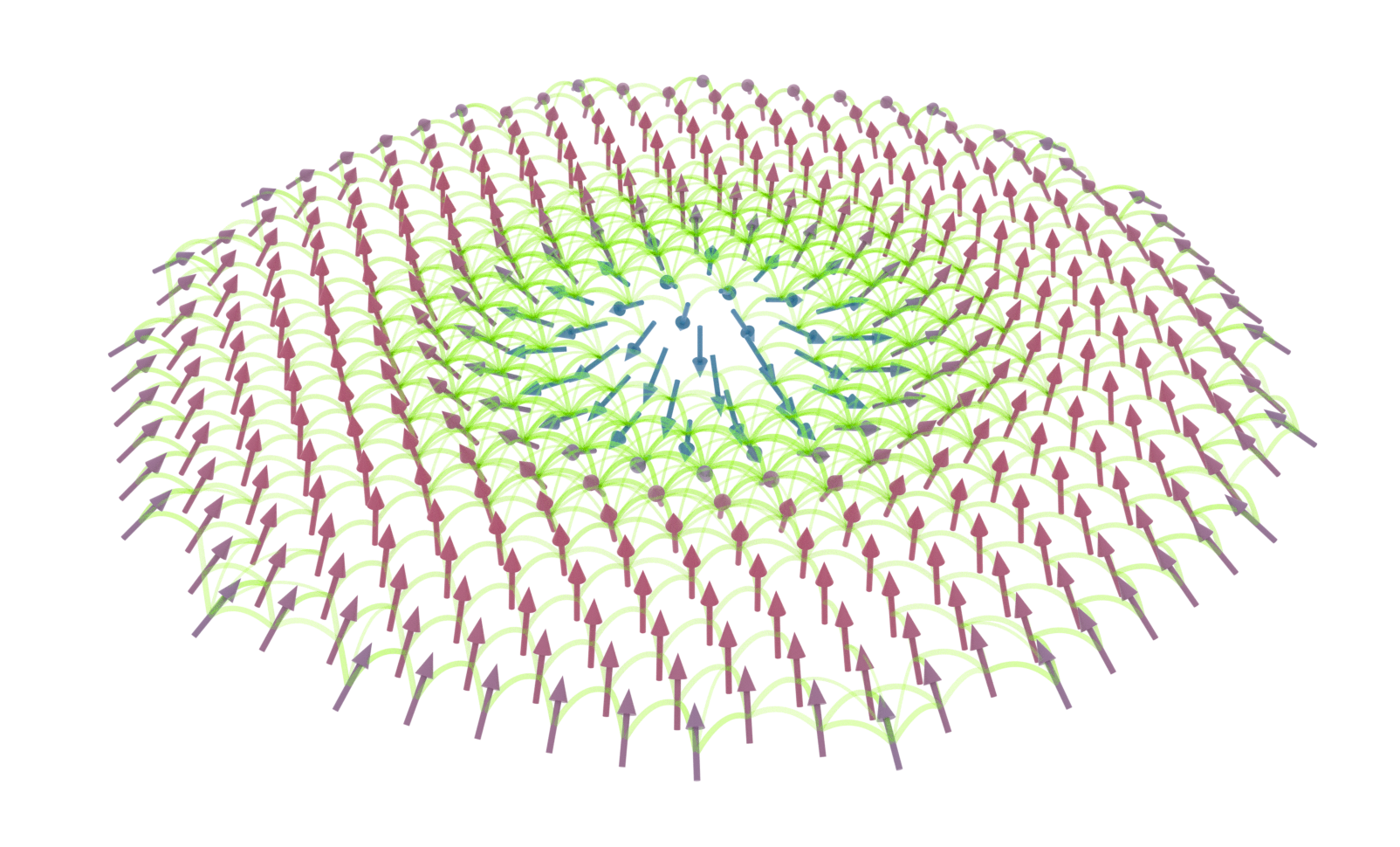
Quantum Spin Model
Concurrence: measure for pair entanglement
 $1^{\rm st}\ \rm n.n.$
$1^{\rm st}\ \rm n.n.$
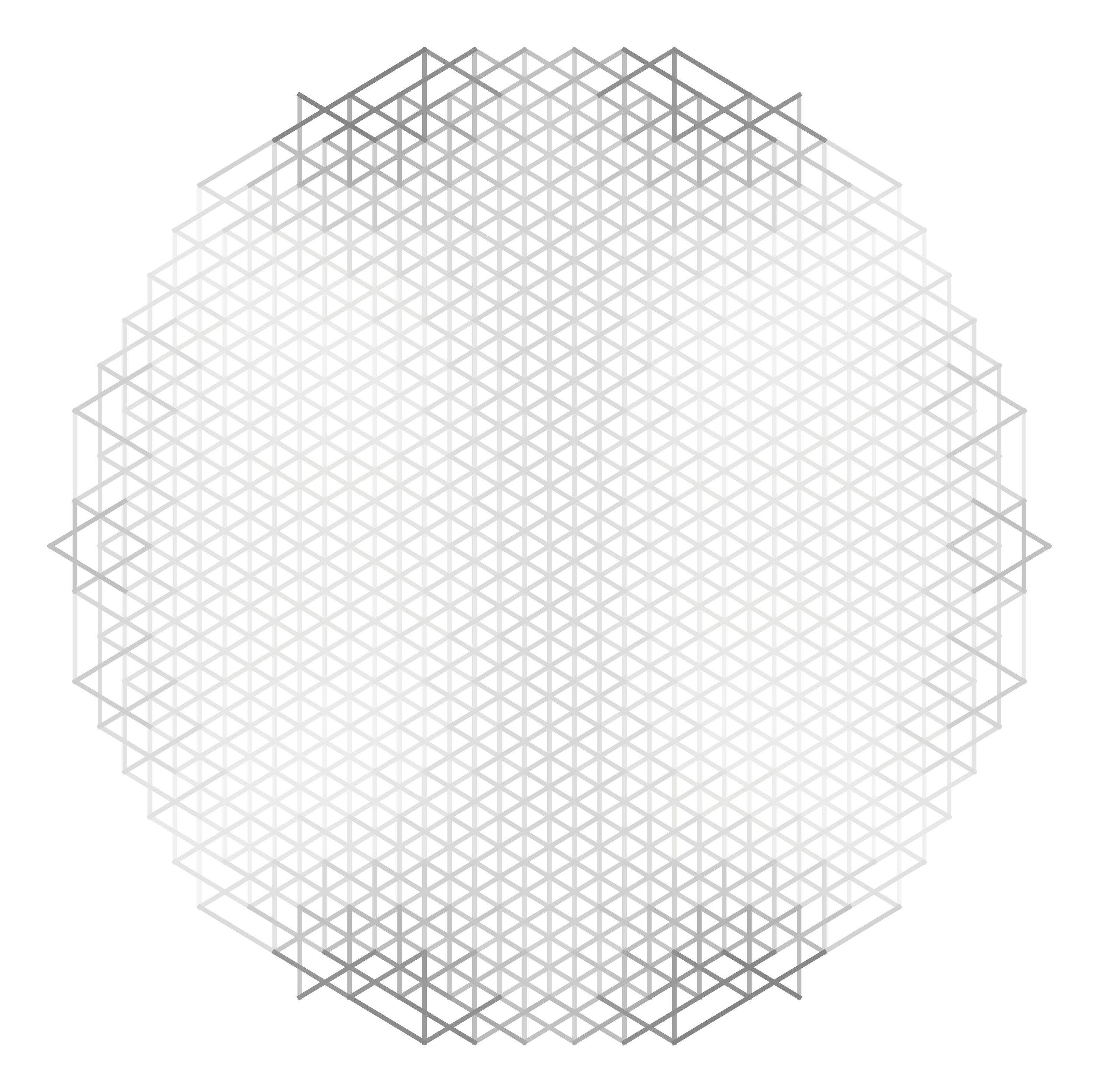 $2^{\rm nd}\ \rm n.n.$
$2^{\rm nd}\ \rm n.n.$
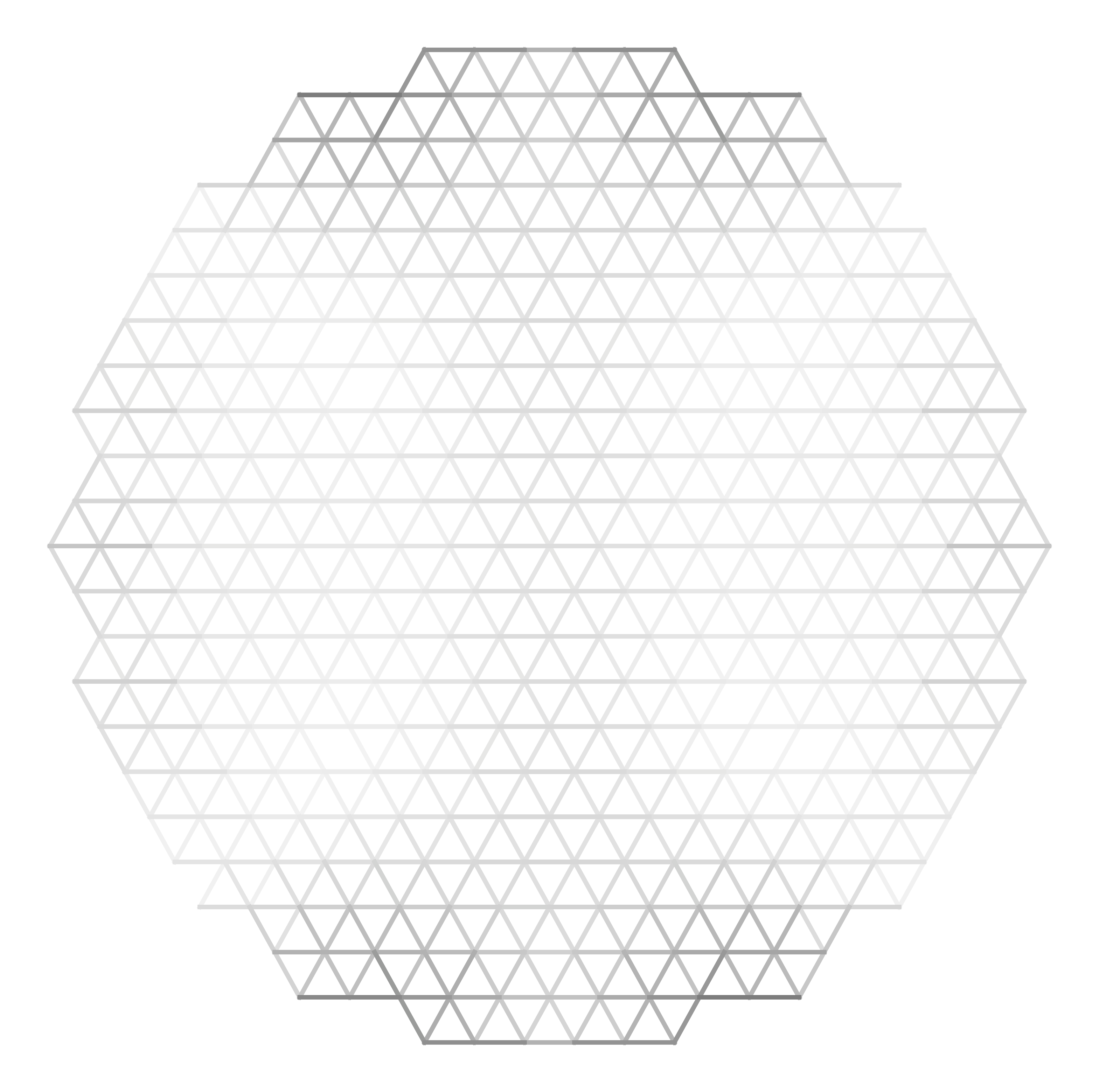 $3^{\rm rd}\ \rm n.n.$
$3^{\rm rd}\ \rm n.n.$
Quantum Spin Model
Concurrence: measure for pair entanglement
 $1^{\rm st}\ \rm n.n.$
$1^{\rm st}\ \rm n.n.$
 $2^{\rm nd}\ \rm n.n.$
$2^{\rm nd}\ \rm n.n.$
 $3^{\rm rd}\ \rm n.n.$
$3^{\rm rd}\ \rm n.n.$
Quantum Spin Model
Concurrence: measure for pair entanglement
 $1^{\rm st}\ \rm n.n.$
$1^{\rm st}\ \rm n.n.$
 $2^{\rm nd}\ \rm n.n.$
$2^{\rm nd}\ \rm n.n.$
 $3^{\rm rd}\ \rm n.n.$
$3^{\rm rd}\ \rm n.n.$
Quantum Spin Model
spin structure factors
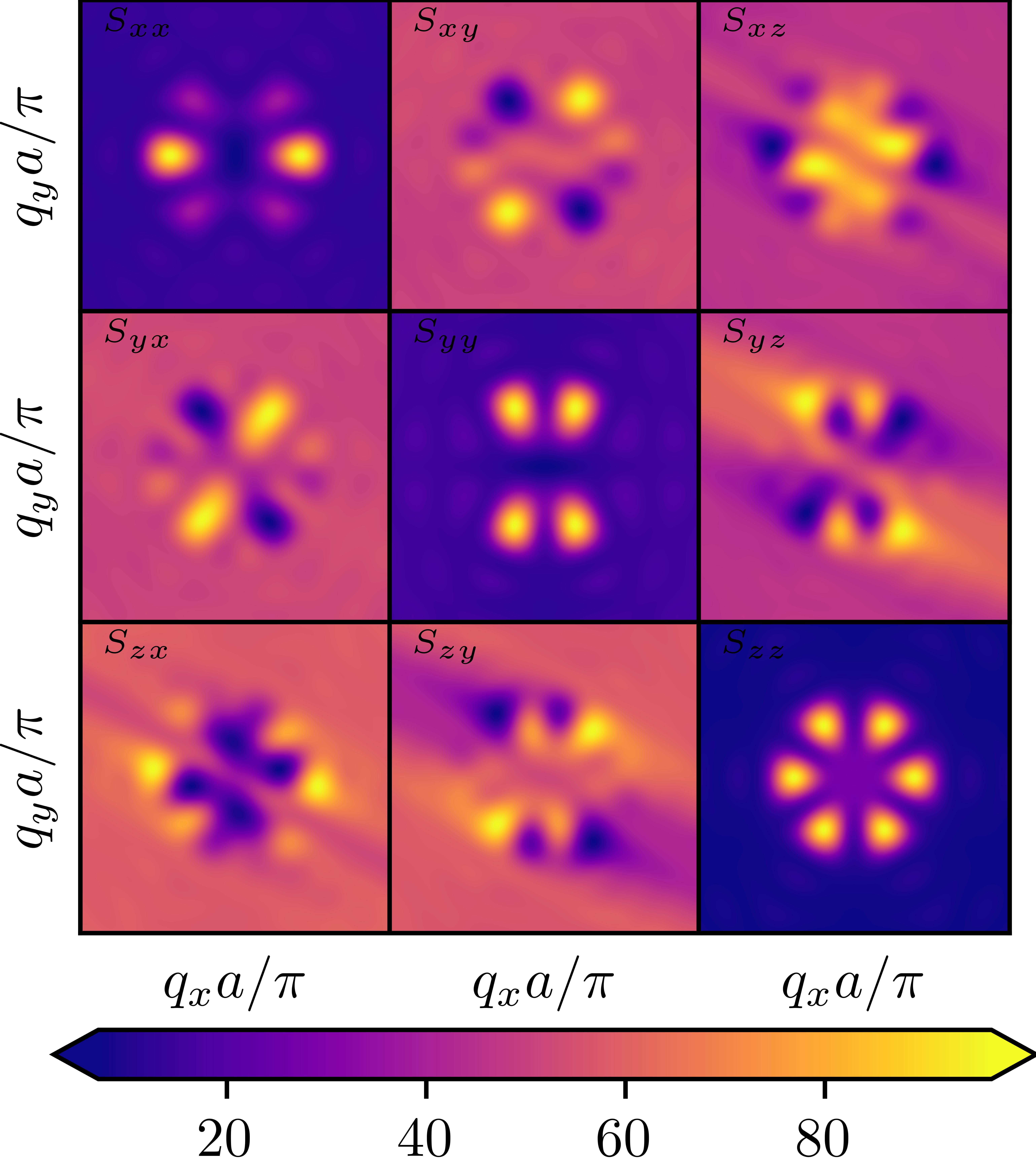 spin spiral
spin spiral
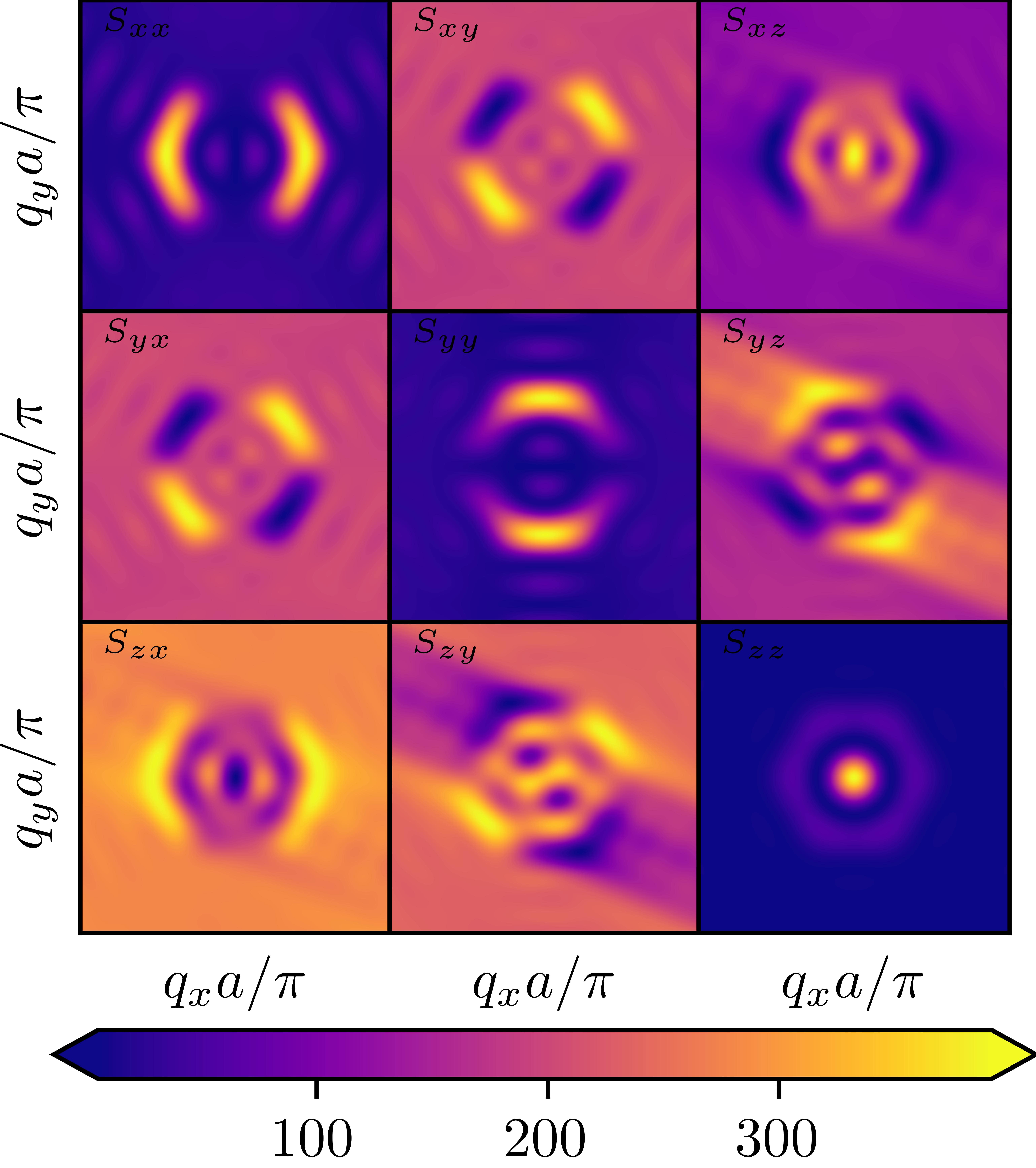 skyrmion
skyrmion
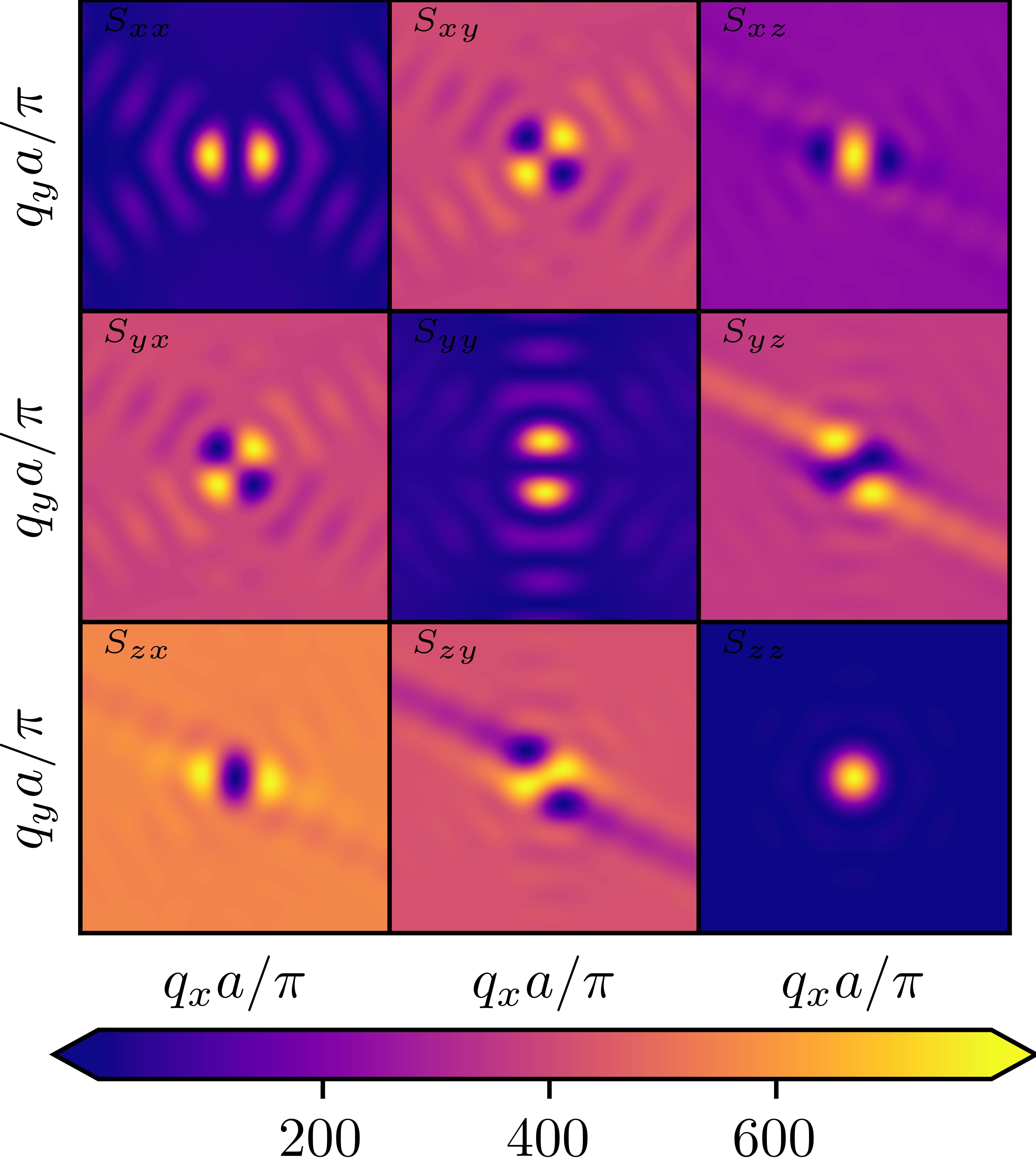 field polarized
field polarized
Quantum Spin Model
neutron scattering cross section
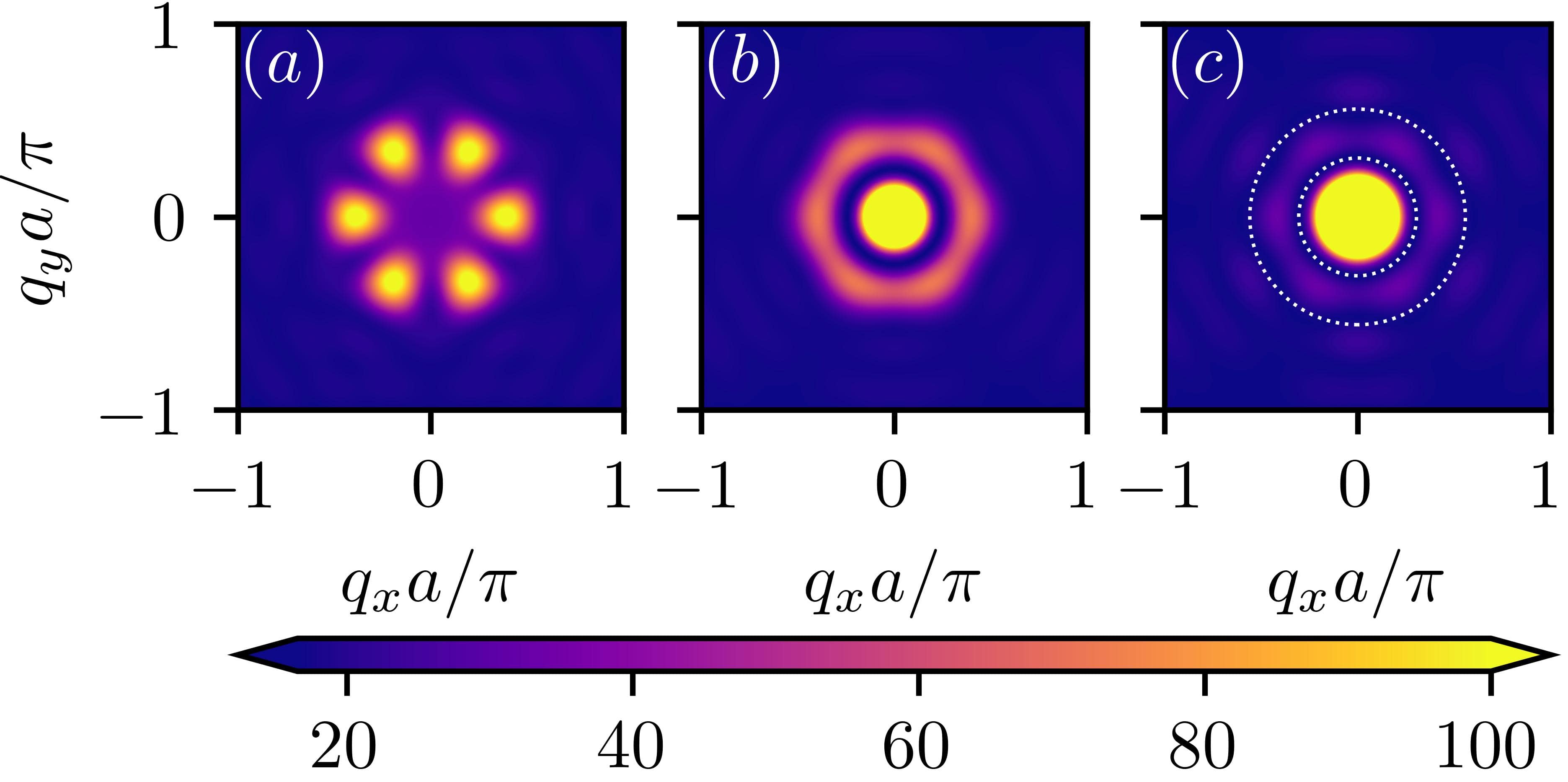
efficient DMRG simulations of quantum skyrmions
quantum skyrmion lattice
domain-wall entanglement
smoking gun signature: spin norm & concurrence
Perspectives
Acknowledgements
 Prof. Dr. Thomas Schmidt
Prof. Dr. Thomas Schmidt
 Prof. Dr. Andreas Michels
Prof. Dr. Andreas Michels
energy convergence
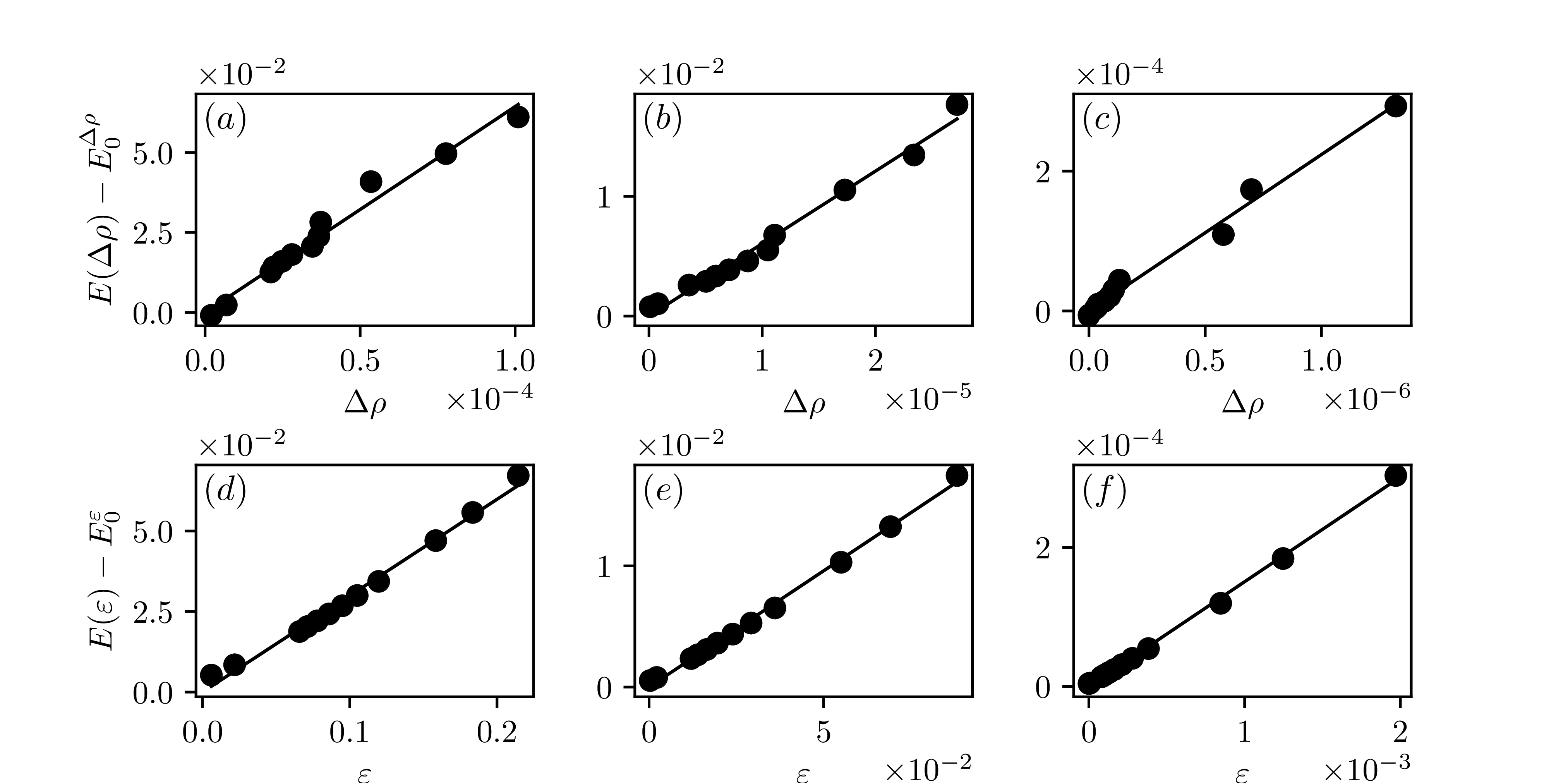
magnetization convergence
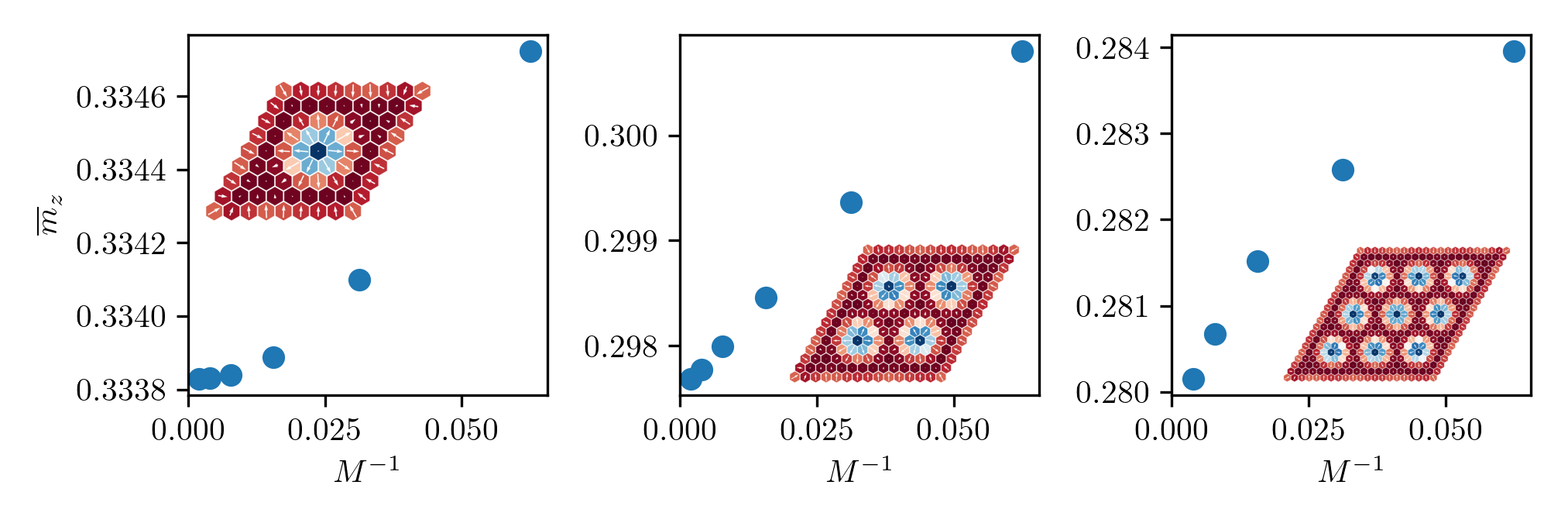
entanglement entropy

magnetization and entropy
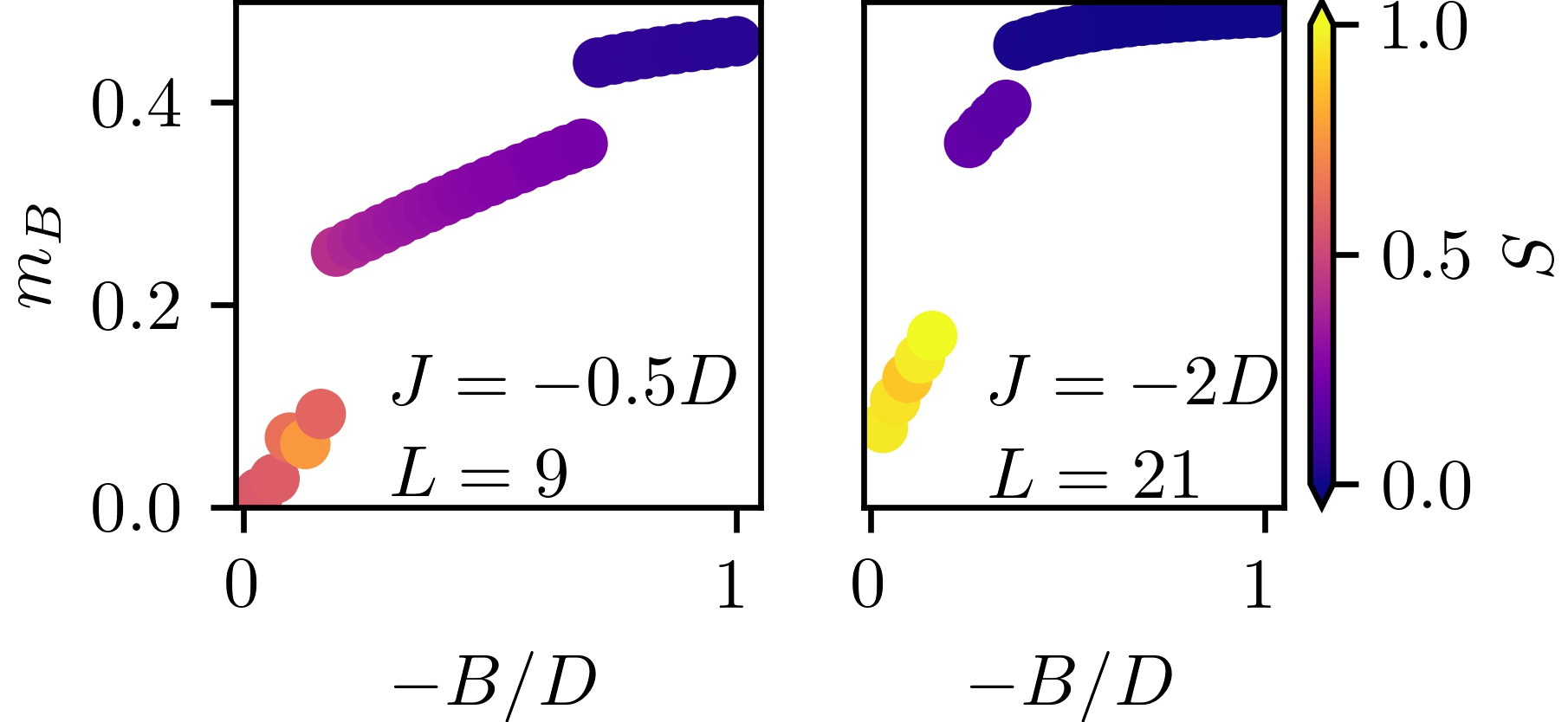
spin norm hexagon
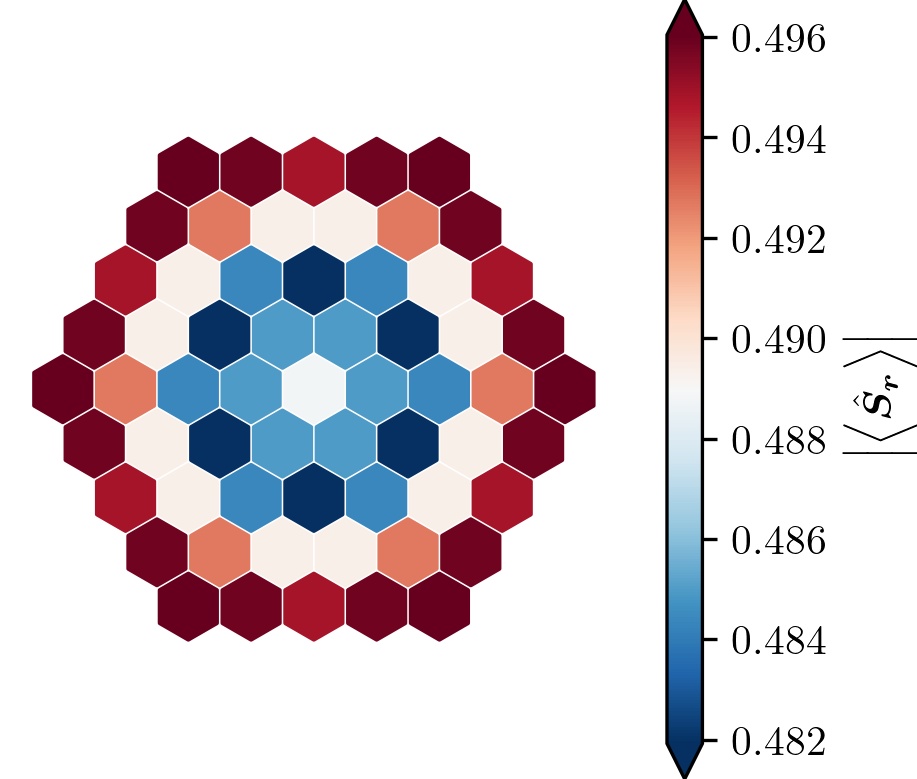
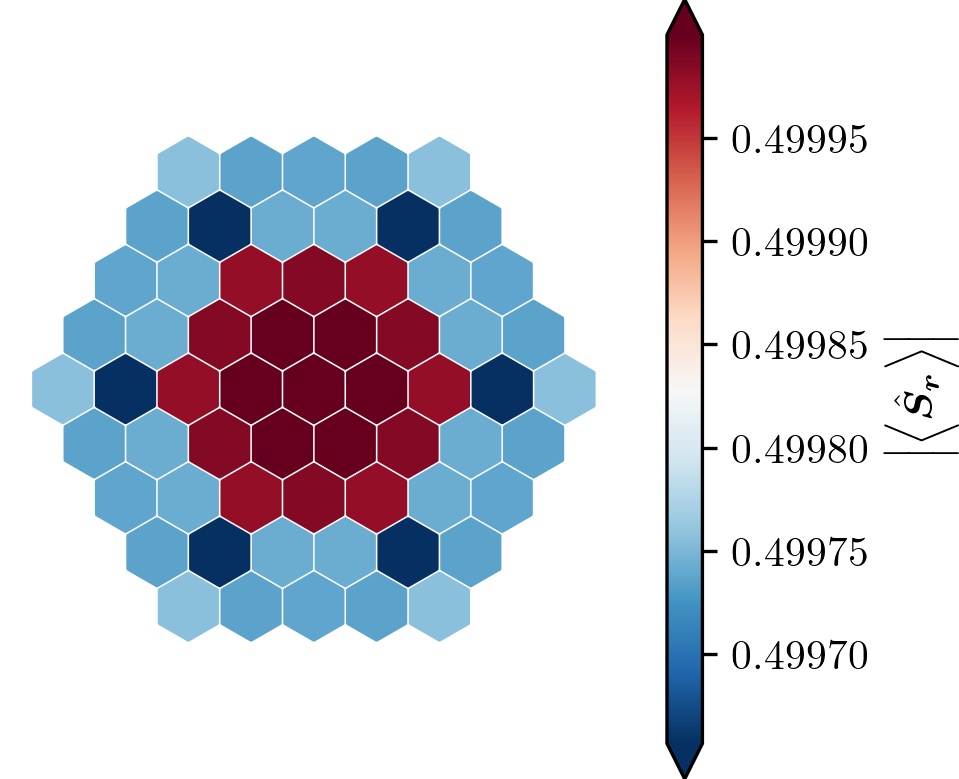
classical low-$E$ spectrum